Интергармоники
Благодаря использованию данного типа управления, прохождение тока через полупроводниковый переключатель обеспечивается в течение всего полного цикла. Таким образом, сигнал тока, протекающего в цепи, не искажается в процессе управления – он является либо синусоидальным (для линейной нагрузки), либо равен нулю.
Интергармоники
Продолжение. Начало статьи см. в журнале «Энергосбережение». 2005. № 6. С. 80–84.
Управление целочисленными периодами тиристорных переключателей
Благодаря использованию данного типа управления, прохождение тока через полупроводниковый переключатель обеспечивается в течение всего полного цикла. Таким образом, сигнал тока, протекающего в цепи, не искажается в процессе управления – он является либо синусоидальным (для линейной нагрузки), либо равен нулю.
На рис. 6 представлен пример управляемых полупроводниковых переключателей в трехфазной конфигурации. Переключение трехфазной нагрузки в точке пересечения фазными напряжениями нулевого уровня приводит к возникновению электрического тока в нейтральном проводе четырехпроводной системы. При одновременном подключении к фазам и к активной нагрузке электрический ток в нейтральном проводе не возникает (рис. 6), однако в случае использования индуктивной нагрузки возникают переходные процессы, связанные с процессами переключения.
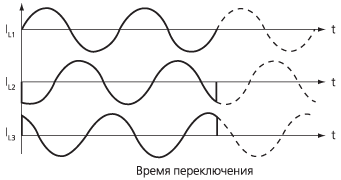 |
Рисунок 6. Формы кривых тока при трехфазной конфигурации в случае использования нейтрального провода для управления целочисленными циклами |
В целях анализа конфигурации, аналогичной той, которая представлена на рис. 7а (с нейтральным проводником), можно ограничиться рассмотрением однофазной схемы (рис. 7б). В дальнейшем будет рассматриваться однофазная цепь с активной нагрузкой, поскольку именно такие схемы наиболее часто используются на практике.
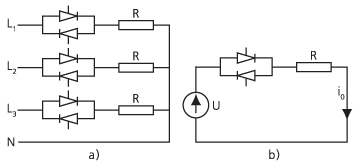 |
Рисунок 7. Регулятор переменного тока |
Полный период управления включает в себя N-циклов проводимости в рамках целого числа циклов М (рис. 8). Величина средней мощности, подводимой к нагрузке, регулируется посредством регулирования величины соотношения N / M. В качестве основы для проведения анализа Фурье (гармонического анализа) период повторяемости формы кривой тока необходимо принять равным Mf1-1, где f1 – это частота напряжения питания, а М – количество циклов.
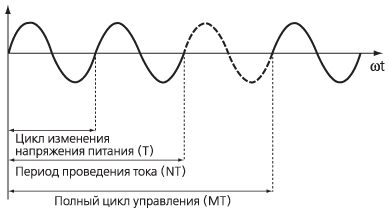 |
Рисунок 8. Форма сигнала тока нагрузки в системе управления целочисленными циклами |
Первой составляющей является промежуточная гармоника сигнала, распложенная на частоте (1/M)f1, которая представляет собой компоненту сигнала тока наименьшей частотой. В примере, представленном на рис. 8, для которого N = 2, M = 3, величина амплитуды данной субгармоники составляет 1/3 частоты напряжения питания. Частоты остальных составляющих кратны частоте этой субгармоники.
Данный тип управления является источником появления субгармоник и промежуточных гармоник, однако не является источником высших гармоник основной составляющей сигнала. При N = 2, M = 3, как показано на рис. 8, амплитуды гармоник равны нулю для n = 6, 9, 12… Спектр сигнала тока, характеризующий данный случай, представлен на рис. 9. Как видно из рис. 9, основными составляющими сигнала являются гармоника частоты напряжения питания и субгармоника, частота которой составляет (2f)/3. Амплитуды гармоник при этом равны нулю.
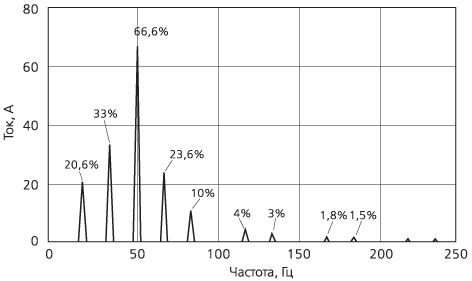 |
Рисунок 9. Спектр сигнала тока при N = 2, М = 3 |
Сетевое сигнальное напряжение питания в электроэнергетических системах
Коммунальные сети электроснабжения предназначены, главным образом, для обеспечения потребителей электроэнергией. Однако поставщики электроэнергии зачастую используют их для передачи системных сигналов управления, предназначенных, например, для регулирования отдельных видов нагрузки (уличное освещение, изменение тарифов, переключение нагрузок, находящихся на значительном удалении) или для передачи данных.
С технической точки зрения, данные сигналы являются источниками промежуточных гармоник, длительность которых составляет от 0,5 до 2 с (в более ранних системах – до 7 с), периодически генерируемых в течение периода времени, равного 6–180 с. В большинстве случаев длительность импульса составляет 0,5 с, продолжительность периода, в течение которого генерируется вся серия импульсов, составляет приблизительно 30 с. Напряжение и частота сигнала устанавливаются заранее, а сам сигнал передается в строго определенные интервалы времени.
Стандартом МЭК 61000-2-1 определяются четыре основные категории сигналов данного типа (МЭК – Международная электротехническая комиссия):
- Пульсирующие сигналы управления – синусоидальные сигналы, лежащие в диапазоне 110–2 200 (3 000) Гц и имеющие частоту 110–500 Гц, они преобладают в современных системах. В основном они используются в профессиональных энергетических системах (а иногда также и в промышленных энергетических системах), в которых действует низкое, среднее, а также высокое напряжение. Амплитуда синусоидального сигнала напряжения изменяется в пределах 2–5 % от значения номинального напряжения (в зависимости от того, какая конкретно система применяется в данном регионе). При возникновении резонанса она может увеличиться до 9 %.
- Сигналы несущей частоты линии электропередачи, лежащие в диапазоне средних частот, – синусоидальные сигналы, лежащие в диапазоне частот 3–20 кГц, в данной категории преобладают частоты 6–8 Гц. В основном они используются в профессиональных энергетических системах. Амплитуда сигнала может достигать 2 % от величины UN.
- Сигналы несущей частоты линии электропередачи, лежащие в диапазоне радиочастот: 20–150 (148,5) кГц (в некоторых странах – до 500 кГц). Они используются в профессиональных, промышленных и в коммунальных энергетических системах, а также применяются в коммерческих целях (дистанционное управление оборудованием и т. д.).
- Сигналы, позволяющие оценить характерис-тики питающей сети, – несинусоидальные маски, накладываемые на форму кривой напряжения и имеющие вид:
а) длинных импульсов (режекция сигнала напряжения длительностью 1,5–2 мс, как правило, в точке перехода напряжения через нулевой уровень);
б) коротких импульсов длительностью 20–50 мкс;
в) импульсов частотой 50 Гц и длительностью, равной одному полному либо половине периода изменения сетевого напряжения.
На рис. 10 представлен пример спектральной характеристики напряжения для системы, в которой осуществляется передача данных на частоте 175 Гц (Uin = 1,35 %). В данном примере в результате взаимодействия с гармоническими частотами происходит генерация других промежуточных гармоник. Составляющие сигнала, амплитуда которых превышает амплитуду второй гармоники, не представляют для нас никакого интереса (они не будут создавать помехи в нагрузке), в то время как промежуточные гармоники с частотой менее 200 Гц могут привести к возникновению серьезных проблем.
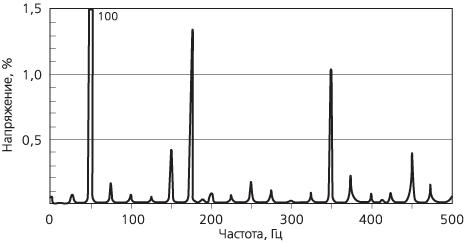 |
Рисунок 10. Результаты БПФ (быстрого преобразования Фурье), примененного к напряжению в процессе распространения сигнала передачи данных (Uin = 1,35 %, f (Uin) = 175 Гц). |
Влияние присутствия промежуточных гармоник
Токи промежуточных гармонических составляющих вызывают гармоническое искажение напряжения в зависимости от величины амплитуд компонент, составляющих сигнала тока, а также от полного сопротивления системы электроснабжения на рассматриваемой частоте. Чем шире диапазон частот компонент, составляющих сигнала тока, тем выше риск возникновения нежелательного явления резонанса, который может увеличить искажение сигнала напряжения и привести к появлению перегрузок и помех в работе оборудования и установок потребителей. Среди наиболее широко распространенных видов непосредственного воздействия промежуточных гармоник можно перечислить следующие:
- тепловой эффект;
- низкочастотные колебания в механических системах;
- возникновение помех в работе люминесцентных ламп и электронного оборудования. На практике, в работе любого оборудования, которое синхронизировано со значением, при котором напряжение питания пересекает нулевой уровень, или с максимальным напряжением, могут возникнуть помехи (рис. 11);
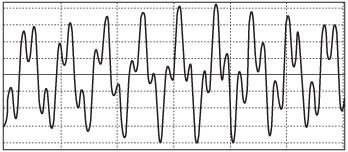 |
Рисунок 11. Кривая напряжения многократно пересекает нулевой уровень вследствие искажения сигнала |
- появление помех в сигналах управления и защиты в линиях электроснабжения. Данное явление на сегодняшний день является самым неблагоприятным видом воздействия промежуточных гармоник;
- возникновение перегрузок в пассивных параллельных фильтрах гармоник высшего порядка;
- возникновение помех в телекоммуникационных линиях;
- акустические помехи;
- насыщение трансформаторов тока.
Наиболее распространенным видом влияния, которое оказывает присутствие промежуточных гармоник, является изменение среднеквадратического значения амплитуды напряжения, а также явление мерцания.
Флуктуации напряжения и эффект мерцания
Значение напряжения питания можно выразить формулами:
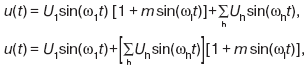
где w1 = 2pf1 и m являются коэффициентами сигнала модуляции, имеющего частоту wi = 2pfi.
Приведенные выше равенства позволяют выявить возможные источники флуктуацийнапряжения, вызванных модуляцией основной составляющей сигнала, которая была произведена при помощи целого числа гармоник. Второй случай не имеет большого практического значения.
Если в формуле будет учитываться только основная составляющая сигнала, то уравнение примет вид:
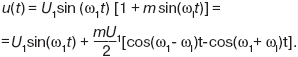
В данном равенстве, помимо основной составляющей, присутствуют две компоненты, частоты которых зависят от частоты модулирующего сигнала и которые расположены симметрично с каждой стороны от основной составляющей частоты. Периодические изменения значения напряжения можно рассматривать как изменения среднеквадратического (или максимального) значения или как результат присутствия промежуточных гармоник боковых полос частот, с помощью которых осуществляется модуляция сигнала напряжения питания.
Так, например, для u(t) = sin(2pft) + m sin(2pfit) (при U1 = 1) максимальное отклонение амплитуды напряжения равняется амплитуде промежуточной гармоники, в то время как отклонение среднеквадратического значения зависит как от амплитуды, так и от частоты промежуточной гармоники. Рис. 12 иллюстрирует максимальное отклонение среднеквадратического значения напряжения, выраженное в процентах, определенное в течение нескольких циклов наблюдения за формой сигнала основной гармоники, которое было вызвано промежуточными гармониками, имеющими различные частоты, но постоянную амплитуду m = 0,2 % от амплитуды основной составляющей сигнала напряжения.
Как видно из рис. 12, влияние промежуточных гармоник, имеющих частоту, превышающую удвоенное значение частоты сигналов, идущих от источника электропитания, невелико по сравнению с воздействием компонент сигнала, которые имеют частоту ниже значения частоты второй гармоники (100 Гц). В случае присутствия промежуточных гармоник появляется риск возникновения флуктуаций напряжения, которые могут вызвать эффект мерцания, если, для заданной частоты, соответствующий уровень превышает предельное значение. Следовательно, если fi ≤ f1, и в особенности, если значения fi лежат близко к значению частоты основной гармоники (f1 ± 15 Гц), то процедура модуляции основной составляющей сигнала будет вызывать отклонение среднеквадратического значения амплитуды напряжения и, соответственно, будет являться источником появления мерцания. Указанное явление можно наблюдать как в лампах накаливания, так и во флуоресцентных лампах, несмотря на то, что сам механизм действия и диапазоны частот, а также допустимые значения амплитуды компонент возмущающих сигналов в этих устройствах абсолютно различны.
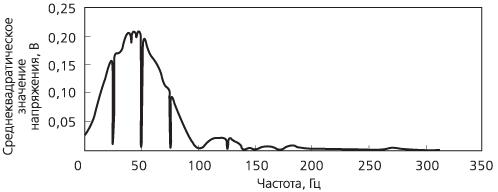 |
Рисунок 12. Зависимость среднеквадратического значения отклонения напряжения от частоты промежуточной гармоники, имеющей постоянную амплитуду (0,2 % от значения амплитуды основной составляющей сигнала) |
В отдельных случаях источниками, являющимися причинами появления эффекта мерцания, могут служить системы передачи сигналов линий электропередачи, которые рассматривались ранее. Несмотря на их небольшую амплитуду, данные сигналы иногда могут вызвать явление мерцания в случае использования очень чувствительных осветительных приборов, таких как энергосберегающие малогабаритные люминесцентные лампы, и в особенности такие лампы, которые обладают индуктивным балластным сопротивлением. Данный вид помех иногда возникает и в источниках света с электронным балластным сопротивлением.
Измерения
Большинство инструментов, с помощью которых проводятся измерения в частотной области, работают исправно только в том случае, когда в измеряемом сигнале присутствуют лишь основные гармоники. В указанных приборах в целях синхронизации измерений с частотой основной составляющей сигнала и снятия сигнала в течение одного или нескольких циклов, осуществляемого с целью проведения его дальнейшего анализа с использованием быстрого преобразования Фурье (БПФ), применяются замкнутые контуры фазовой автоподстройки частоты. Благодаря использованию замкнутого контура фазовой автоподстройки частоты образцы сигналов, «измеренных в течение одного цикла», могут дать точное представление о спектре сигнала только в том случае, если в нем отсутствуют промежуточные составляющие. Если же присутствуют иные негармонические частоты (в период проведения измерений) и/или в рассматриваемом временном интервале форма подвергающегося дискретизации сигнала не является периодической, то сразу возникают трудности с интерпретацией полученных результатов.
Основным инструментом для проведения анализа является использование преобразования Фурье (ПФ). На практике анализ сигнала проводится в течение ограниченного интервала времени (временное окно для измерения – Tw) с использованием ограниченного числа выбранных составляющих (или дискрет) (М) реального сигнала. Результаты применения дискретного преобразования Фурье (ДПФ) зависят от выбранных значений Tw и М. Обратной величиной для Tw является основная частота преобразования Фурье – fF. ДПФ применяется к реальному сигналу в рамках определенного временного окна; сигнал, возникающий вне данного временного окна, не обрабатывается, однако, считается, что его форма идентична форме сигнала, существующего в пределах временного окна. Таким способом реальный сигнал заменяется виртуальным сигналом, который является периодическим, с периодом, равным ширине временного окна.
При анализе кривых периодических сигналов бывает необходимо осуществить синхронизацию периода проведения анализа с периодом основной составляющей сигнала (а также с гармониками), что не вызывает никаких затруднений. Тем не менее, в процессе проведения анализа промежуточных гармоник возникают более сложные проблемы. Частоты составляющих промежуточных гармоник не являются целочисленными кратными значениям частоты основной гармоники, к тому же они зачастую подвержены изменениям во времени, что еще больше затрудняет проведение измерений.
Вследствие присутствия как гармонических составляющих, так и промежуточных гармоник значение частоты преобразования Фурье, которое представляет собой наибольший общий делитель для всех составляющих частоты, присутствующих в сигнале, отличается от значения собственной частоты напряжения питания и, как правило, является небольшим. В данной ситуации возникают две проблемы:
- минимальное время выборочного исследования сигнала может оказаться большим, также как и количество отобранных образцов сигналов;
- представляется затруднительным предсказать значение основной частоты преобразования Фурье, поскольку не все частотные составляющие сигнала известны априори.
Данный факт может быть проиллюстрирован следующими примерами. Сигнал, который необходимо проанализировать, представляет собой совокупность основной составляющей (50 Гц), промежуточной гармоники (71,2 Гц) и гармоники (2 500 Гц). Основная частота преобразования Фурье равняется 0,2 Гц, что намного ниже частоты основной составляющей сигнала. Соответствующий период составляет 5 с, и, следовательно, минимальное допустимое время выборочного исследования также составляет 5 с. Принимая во внимание тот факт, что частота дискретизации равняется 10 кГц, что фактически является минимально возможным значением, выбранным в соответствии с критерием устойчивости Найквиста (прил. Б), минимально необходимое количество отобранных компонент М будет составлять 50 000. Если бы промежуточная гармоническая составляющая (71,2 Гц) отсутствовала, то минимальное время измерения составило бы 20 мс, а количество исследуемых компонент было бы равно 200.
Сигнал, который необходимо проанализировать, представляет собой совокупность основной составляющей (50 Гц) и гармоники (2 500 Гц), амплитуда каждой из них изменяется по синусоидальному закону с частотой 0,1 и 5 Гц соответственно. Следствием проведения подобных процедур модуляции является появление четырех промежуточных гармоник на частотах 49,9; 50,1; 2 495 и 2 505 Гц. Основная частота преобразования Фурье будет равняться 0,1 Гц, минимальное время выборочного исследования будет составлять 10 с, а М = 100 000.
При практическом применении, в силу определенных ограничений, свойственных оборудованию и программному обеспечению, количество исследуемых образцов М не может превышать определенное максимальное количество, и, следовательно, время измерения также будет ограниченным. Использование значения времени измерения, отличного от длительности основного периода преобразования Фурье, приводит к нарушению непрерывности сигнала на отрезке времени между началом и окончанием временного окна измерения. Это приводит к возникновению ошибок при идентификации составляющих сигнала, данное явление известно под названием рассеяния спектра. Данную проблему можно решить посредством применения к сигналу, изменяющемуся во времени, «взвешенного» значения временного окна перед началом проведения анализа с помощью БПФ. На практике используются два типа окон измерения: прямоугольное окно и окно Хенинга (прил. А).
Приложение А
Преобразование Фурье представляет собой наиболее популярный метод, используемый для спектрального анализа сигнала. В фундаментальной теории спектрального анализа делается допущение о том, что анализ проводится в течение периода времени, лежащего в пределах [-∞; +∞]. В результате применения дискретного преобразования Фурье (ДПФ) или его разновидности, быстрого преобразования Фурье (БПФ), могут неожиданно появиться побочные составляющие спектра анализируемого сигнала. Указанное явление возникает вследствие того, что ДПФ и БПФ применяются к ограниченному количеству отбираемых составляющих сигнала, т. е. только к части реального сигнала. Полученный и реальный спектры будут идентичны только в том случае, если сигнал является периодическим, а промежуток времени, в течение которого производился анализ, включает целое число полных периодов сигнала. При реализации на практике данное условие выполнить очень сложно.
Результаты, представленные на рис. А.1 и А.2, наглядно иллюстрируют то, как может выглядеть реальный спектр сигнала. Для одного и того же сигнала были получены различные спектры вследствие того, что период наблюдения в случае, проиллюстрированном на рис. А.2, был на 2,5 % длиннее. В библиографии данное явление именуется рассеиванием спектра. Иными словами, это явление можно описать как переход части энергии от основной спектральной линии на боковые спектральные линии. Данный феномен может быть интерпретирован следующим образом. Отбор образцов для проведения анализа при помощи ДПФ можно сравнить с усилением реального сигнала бесконечной длительности посредством применения прямоугольного окна, соответствующего продолжительности периода наблюдения, рис. А.3.
Чтобы ограничить рассеивание спектра, необходимо добиться того, чтобы величины (амплитуды) анализируемого сигнала в начале и в конце периода выборочного исследования не изменялись слишком быстро.
На рис. А.4 показано, как следует использовать временное окно для анализа сигнала.
На рис. 15 показано, какое влияние применение представленных методов оказало на спектр сигнала по сравнению с примером, проиллюстрированным на рис. А.2. В данном примере использовалось окно Хенинга. Результатом его применения явилось уменьшение количества ненулевых спектральных линий, а сам спектр приблизился к реальному спектру, как показано на рис. А.1.
Количество окон, применяемых при проведении анализа с помощью ДПФ, указано в приведенной в данном документе библиографии. Наиболее популярными среди них являются (рис. А.6):
- треугольное окно, аналогичное окну Барлетта;
- окно Хенинга;
- окно, поднятое по закону косинуса: либо окно Хенинга, либо окно Хэмминга.
Данные окна наиболее часто применяются для измерительных приборов. Их использование не устраняет проблемы, связанные с рассеиванием спектра, однако позволяет существенно снизить отрицательное влияние, которое оказывает ограничение интервала наблюдения. Это становится особенно очевидным благодаря улучшению разрешения спектра сигнала.
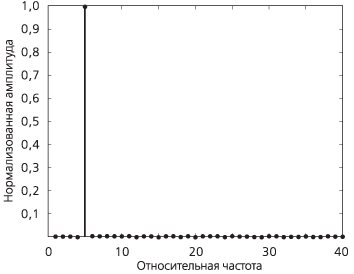 |
Рисунок А.1. Модуль спектра сигнала; для проведения анализа использовалось ровно 4 цикла |
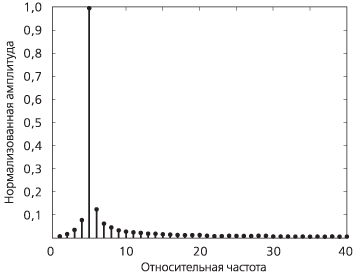 |
Рисунок А.2. Модуль спектра сигнала; для проведения анализа использовались 4.1 цикла |
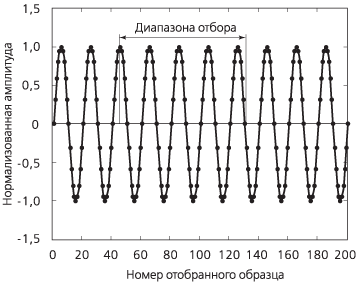 |
Рисунок А.3. Отбор образцов при проведении анализа спектра с применением ДПФ |
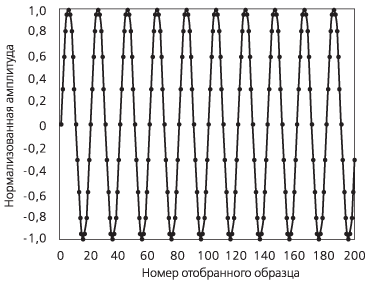 |
Рисунок А.4а. Изображение образцов, отобранных для проведения анализа |
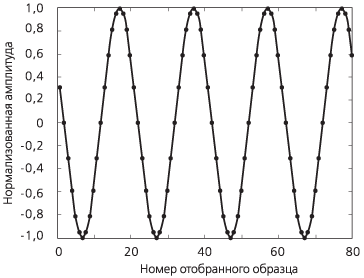 |
Рисунок А.4б. Результат применения временного окна, для которого устанавливается значение yi = wi*xi, где: yi = сигнал в пределах установленного временного окна, xi,= измеряемые образцы; wi = вырезающая функция, значение i изменяется от 1 до N (количество отобранных образца). |
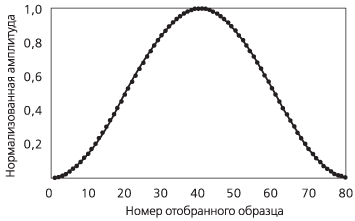 |
Рисунок П.1.4в. Анализ спектра с применением ДПФ |
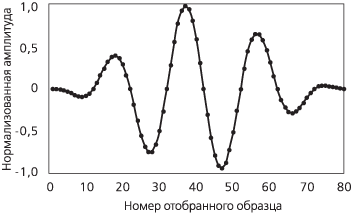 |
Рисунок П.1.4г. Анализ спектра с применением БПФ |
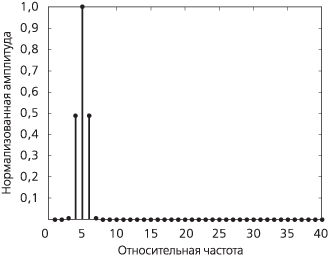 |
Рисунок А.4д. Временные окна, используемые для анализа спектра сигнала |
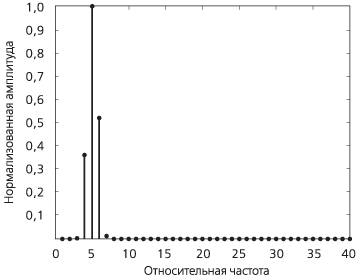 |
Рисунок А.5. Пример применения окна Хэмминга для проведения анализа с использованием ДПФ |
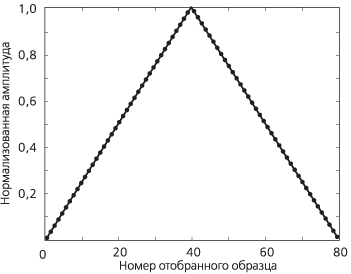 |
Рисунок А.6а. Треугольное окно |
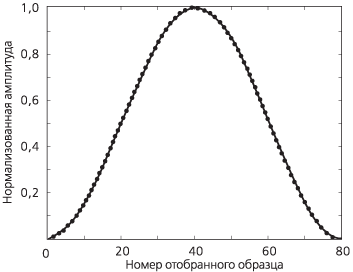 |
Рисунок А.6б. Окно Хенинга |
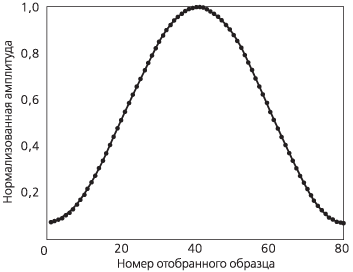 |
Рисунок А.6в. Окно Хэмминга |
Перепечатано с сокращениями из издания Европейского института меди «Прикладные аспекты качества электроэнергии»
Редактор перевода В. С. Ионов
Продолжение в следующем номере

Статья опубликована в журнале “Энергосбережение” за №3'2006
Подписка на журналы
















