Расход теплоты при обогреве труб теплоспутниками
Колесник Иван Юрьевич, инженер проектировщик, проектный институт ООО «РН»-УфаНИПИнефть», отдел отопления и вентиляции.
В работе рассматриваются процессы теплообмена внутри изоляционного кожуха между греющим трубопроводом-спутником и обогреваемым продуктопроводом. Разработан и реализован алгоритм, который позволяет количественно определить составляющие этого теплообмена и получить эксплуатационные характеристики теплоизоляционной конструкции с теплоспутником. За основу алгоритма взят простой инженерный метод, описанный в [1] и основывающийся на методах расчета теплообмена теории подобия.
Очевидно, что при спутниковом обогреве часть тепла неизбежно теряется в окружающую среду, в связи с чем возникают естественные вопросы:
- какова доля этих потерь,
- каков полезный эффект,
- какова доля этого полезного эффекта.
Задачи предлагаемого исследования:
1. Получить удобный метод расчета. Обеспечить возможность быстро получать технико-эксплуатационные характеристики систем спутникового обогрева (расход энергии, потери, их соотношение).
2. Оценить процессы теплопередачи в изоляционном кожухе.
3. Создать базу для корректного сравнения теплоспутникового и электрического обогрева трубопроводов.
Описание метода.
В данной работе использован инженерный метод, описанный в справочнике [1].
Метод основан на теории подобия и детальном расчете геометрических размеров сечения кожуха.
Теплопотери вычисляются по известной формуле

Самая важная составляющая – коэффициент теплоотдачи – определяется по параметрическим уравнениям связывающим числа подобия. Вид уравнений зависит от характера процесса (естественный, вынужденный и т.д.).
Для простейших случаев выведены формулы коэффициентов теплопередачи,
Для плоской поверхности

Вычисление площади трубы или плоской поверхности тоже не представляет сложностей.
Наличие спутника изменяет геометрию сечения, для этого случая теоретических формул нет, определение площади поверхности тоже усложняется.
Идея метода – представить процесс, как сумму элементарных, теоретически описанных: через плоскости и дуги окружностей.
Выделены 5 таких элементарных направлений переноса тепла:
- от продуктопровода через изоляцию наружу (Q1)
- из замкнутого пространства внутри теплоизоляционного кожуха к поверхности продуктопровода (Q2),
- от поверхности спутника внутрь кожуха (Q3),
- из кожуха через изоляцию наружу (Q4),
- от спутника через изоляцию наружу (Q5).
Все составляющие вычисляются по формуле (1).
Этот, своего рода, баланс представлен на рисунке 1.
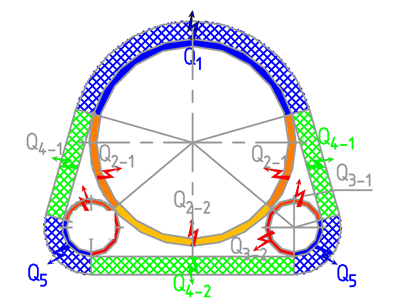
Рисунок 1 – Составляющие переноса теплоты в кожухе.
Формулы для коэффициентов теплопередачи приведены, величины необходимых коэффициентов теплоотдачи даны в описании метода [1] (можете видеть их справа в недоступных для редактирования ячейках); теплоотдачей внутри трубопровода, транспортирующего жидкую среду, в соответствии с указаниями [4] можно пренебречь. Определение геометрических параметров сводится к расчету треугольников, нахождению размеров и углов по их тригонометрическим функция по формулам из школьного курса в зависимости от расчетной схемы (формы) кожуха (таковых 6).
В [1] рекомендуется предусматривать зазор между спутником и изоляцией, величиной 10 мм. Не очень понятно, как осуществить это технически, в других источниках об этом не упоминается, однако возможность учесть этот зазор предусмотрена.
С учетом этих двух факторов (количество спутников и наличие зазора) выявлены и рассмотрены варианты расчетной схемы, представленные на рисунке 2.
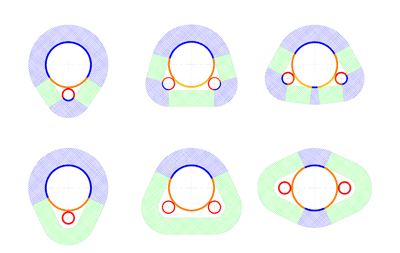
Рисунок 2 – Варианты расчетной схемы.
Зная диаметры и количество труб, можно определить телпопотери в местах, где труба покрыта изоляцией. Но для расчета величин теплообмена между воздухом в кожухе и трубами и между воздухом и окружающей средой (сквозь кожух) необходимо знать температуру в кожухе.
Все три составляющие зависят от температуры в кожухе, а их сумма представляет собой уравнение баланса (закона сохранения в этом кожухе).
Из этого уравнения температура в кожухе выражается в виде следующего выражения
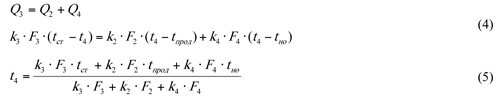
Соответствующие - коэффициент теплоотдачи, площадь и температура i-й поверхности, обращенной в замкнутое пространство кожуха.
Баланс теплопотоков в воздушном пространстве в кожухе схематично показан на рисунке 3.
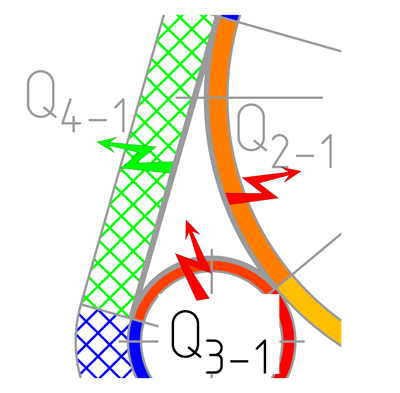
Рисунок 3 – Составляющие теплового баланса изолированного воздушного объема в кожухе.
Форма этого выражения может несколько меняться в зависимости от количества составляющих баланса кожуха, которое определяется конструкцией кожуха.
Т.о., исходными данными являются
- температуры, °С;
- свойства изоляции, мм;
- диаметры продуктопровода, спутников, расстояние между спутниками, мм;
- количество спутников (один или два);
- величины коэффициентов теплоотдачи на поверхностях всех труб и по обеим сторонам изоляции, Вт/м?•°С.
Результаты расчета таковы:
- величина теплоотдачи с поверхности спутника в кожух, Вт/пм,
- полная теплоотдача спутника, учитывающая теплопотери спутника через изоляцию, Вт/пм;
- количество теплоты, воспринимаемое поверхностью продуктопровода из кожуха, Вт/пм;
- разность количества теплоты, воспринимаемого продуктопроводом из кожуха и теряемым им через изоляцию, Вт/пм (т.н. баланс);
- суммарные теплопотери через поверхность изоляционной конструкции, Вт/пм,
- отношение полезного эффекта к затраченному (воспринятого тепла к отданному в пространство кожуха), %;
- температура внутри кожуха, °С;
- площадь сечения изоляции, м?, для оценки ее объема;
- наружный периметр кожуха, м.
По величине тепловых потоков отдаваемых или воспринимаемых трубопроводом можно с учетом расхода жидкости в трубе и теплоемкости судить об изменении ее температуры.
По величине баланса тепла продуктопровода можно сделать косвенный вывод о том, достаточна ли мощность нагрева (размер спутника).
Алгоритм метода имеет вид, приведенный на рисунке 4.
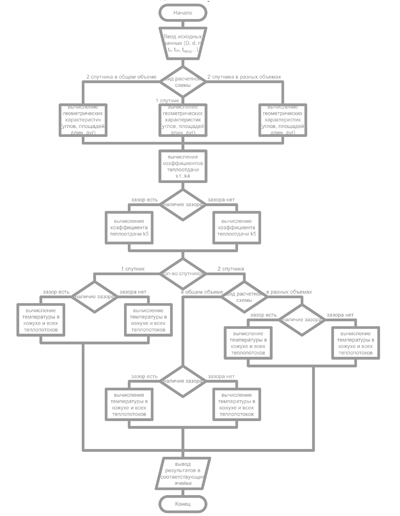
Рисунок 4 – Блок-схема алгоритма
Алгоритм далеко не самый эффективный, в трех местах проверяется почти одно и то же условие. Чтобы быть уверенным в результатах я просчитал вручную 6 вариантов (по одному каждой схемы), а потом приводил код в соответствие со своими результатами.
Алгоритм реализован на MS VisualBasic. Вид рабочего окна представлен на рисунке 5.
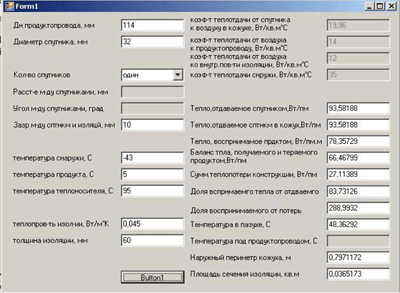
Рисунок 5 – Вид рабочего окна.
Получив метод расчета, я стал анализировать изменение параметров и составляющих процесса в зависимости от разных влияющих факторов.
В результате использования данного метода получено большое количество данных, характеризующих переноса тепла в кожухе и позволяющих его проанализировать. Большинство зависимостей построено для трубы с наружным диаметром 114 мм, обогреваемой спутником с наружным диаметром 32 мм без зазора. Результаты обработки полученных расчетных данных приведены на рисунках 6..13.
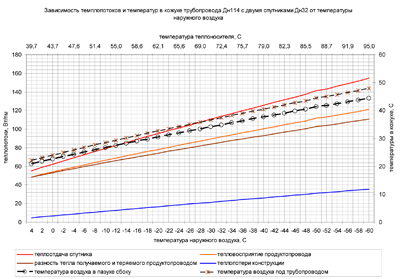
Рисунок 6 – Зависимость теплопотоков при обогреве трубопровода с наржуным диаметром 114 мм одним спутником с наружным диаметром 32 мм.
По нижней оси температура наружного воздуха, по верхней – температура теплоносителя, по левой теплопотоки, а по правой доля тепла, воспринимаемого продуктопроводом от отдаваемого спутником (зеленая линия). Температуры наружного воздуха и теплоносителя связаны линейно, т.к. тепловая нагрузка на источнике регулируется качественно в зависимости от температуры наружного воздуха.
Можно сделать вывод, что с понижением температуры наружного воздуха доля полезно используемого тепла уменьшается, хотя по абсолютной величине все составляющие баланса растут.
При этом температура в кожухе, как и температура теплоносителя, увеличивается, и это видно на следующем графике, где вспомогательная ось справа показывает значения температуры в пазухах и под трубопроводом.
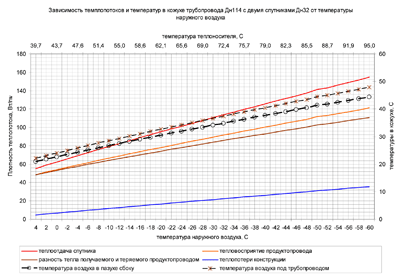
Рисунок 7 – Зависимость теплопотоков при обогреве трубопровода с наружным диаметром 114 мм двумя спутниками с наружным диаметром 32 мм.
Изменение доли полезно используемого тепла имеет тот же характер, что и на предыдущем графике (убывающий), поэтому она здесь не показана, хотя по абсолютной величине несколько выше, чем при обогреве трубы одним спутником.
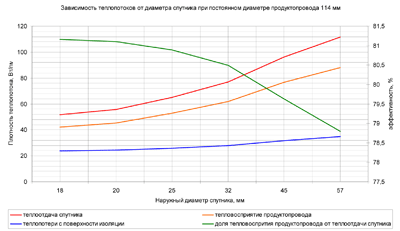
Рисунок 8 – Зависимость величин теплопотоков от диаметра спутника при постоянном диаметре продуктопровода.
Возможна ситуация, когда тепловосприятие продуктопровода может приближаться к теплопотерям и даже быть ниже, чем они. Т.е. оранжевая кривая может и пересекать горизонтальную ось, и баланс тепла в продуктопроводе будет отрицательным, когда спутник не обеспечивает восполнения теплопотерь. Это возможно при высокой температуре продукта или малой толщине изоляции. В целях экономии следует предусматривать работу спутника в условиях чуть выше этой границы. Не следует допускать перерасхода тепла (на картинке тепловосприятие трубы от 40 Вт/пм и выше), надо стараться минимизировать баланс, дабы не греть продукт впустую, когда этого не требуется. Но нельзя сказать до какой степени можно к этой границе приблизиться, т.к. данный метод не позволяет анализировать температурные поля в изоляции или продуктопроводе. Теоретически при большом перепаде (градиенте) температур возможна ситуация, когда обогреваемый трубопровод будет получать больше тепла, чем отдавать, но перемешивание в трубе будет недостаточным и где-то в верхней части сечения образуется лед (в теории). Но отсутствие перемешивания должно, наверное, означать, что поток в трубе ламинарный, чего на практике не должно быть. Однако, я не стану говорить, насколько тепловосприятие должно превышать теплопотери. Тем не менее, границу эту отловить можно.
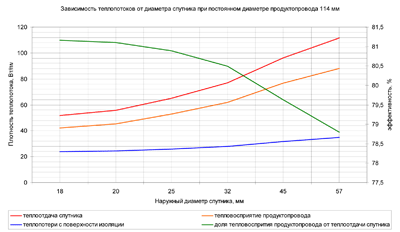
Рисунок 9 – Зависимость величин теплопотоков от диаметра продуктопровода при постоянном диаметре спутника.
Этот и предыдущий рисунки указывают на то, что следует стремиться к меньшему диаметру спутника.
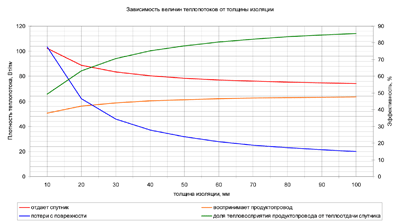
Рисунок 10 – Зависимость величин теплопотоков от толщины изоляции.
Здесь все предсказуемо, скажу только, что температура в кожухе изменяется также, как эффективность.
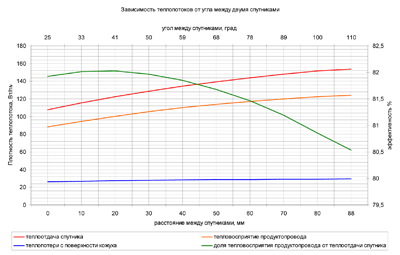
Рисунок 11– Зависимость величин теплопотоков от угла между спутниками.
Всегда было любопытно. График построен для случая обогрева трубопровода Ду100 спутниками Ду25. Можно сделать неожиданный вывод, что имеет место некоторый оптимальный угол. Когда расстояние между спутниками мало, вероятно, площадь поверхности продуктопровода, обращенная в этот промежуток очень мала, а с увеличением расстояния эта площадь и, соответственно тепловосприятие, растут, но после некоторого оптимума рост теплопотерь наружу через изоляцию имеет определяющее значение.
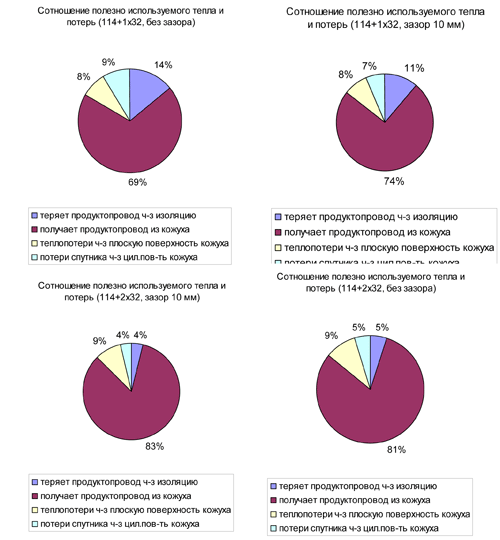
Рисунок 12 – Соотношение между теплопотоками в кожухе при температуре наржуного воздуха -43 °С, температуре теплоносителя 95 °С, температуре продуктопровода 5°С и толщине изоляции 60 мм при наличии или отсутствии зазора.
Из этих диаграмм можно заключить, что зазор, о котором упоминается в [1], повышает эффективность обогрева. Сравнивать обогрев одним или двумя спутниками, думаю, не стоит, т.к. абсолютные цифры различаются почти в два раза.
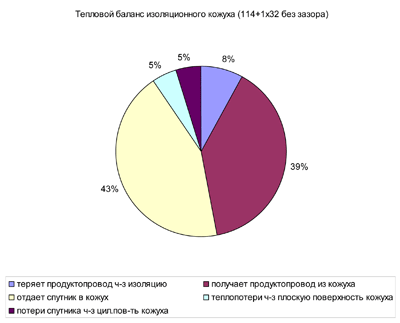
Рисунок 13 – Составляющие теплового баланса кожуха при температуре наржуного воздуха -43 °С, температуре теплоносителя 95 °С, температуре продуктопровода 5°С и толщине изоляции 60 мм при отсутствии зазора.
Это все касалось метода, основные этапы которого, я повторю:
- разбиение поверхности теплообмена на элементарные составляющие;
- вычисление их геометрических размеров;
- расчет температур внутри кожуха;
- вычисление теплопотоков.
Спорные моменты
Размер, коэффициент теплопередачи и разность температур одинаково влияют на теплопередачу (входят в уравнение в одинаковой степени). Но размер неизменен, температуры тоже, как правило, заданы или изменяются незначительно.
Коэффициенты теплоотдачи взяты из [1], где приведены без особых комментариев, но влияние этого коэффициента пропорциональности велико, поэтому следует проверить пределы его изменения.
В теории подобия коэффициент теплопередачи определяется из критериальных уравнений, связывающих числа подобия. Это означает, что коэффициент теплопередачи зависит от размеров, скорости, многих теплофизических параметров среды, которые, в свою очередь, зависят от температуры и давления и т.д.
Сразу скажу, что цифры, сходные с рекомендуемыми, мне удалось получить только для теплоотдачи на наружной поверхности. Коэффициенты теплоотдачи внутри получились примерно в три-шесть раз меньше приведенных. Вероятно, автор [1] использовал другие зависимости, описывающие теплообмен в кожухе, а может быть он приводит экспериментальные значения, т.к. аналитически нельзя учесть возможность накопления какой-нибудь пыли, окалины между трубами, которые неизбежно влияют на процесс. По части теплоотдачи внутри доверимся справочнику.
Коэффициент теплоотдачи при вынужденном омывании поверхности воздухом (ветром) вычисляется при величине числа Рейнолдса более 1000 по формуле (9)

На рисунках 14 и 15 приведены графики изменения коэффициентов теплоотдачи, построенные по приведенным зависимостям.
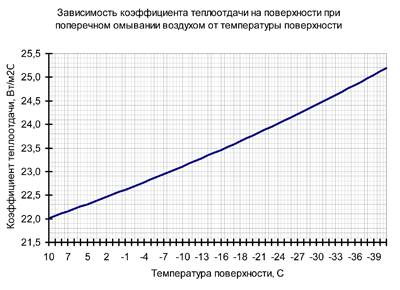
Рисунок 14 – Зависимость коэффициента теплоотдачи на наружной поверхности от температуры
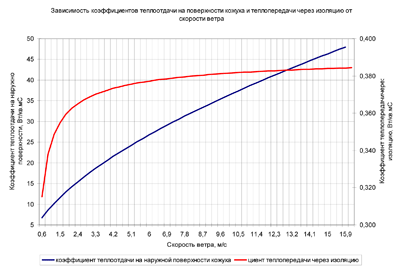
Рисунок 15 – Зависимость коэффициента теплоотдачи на наружной поверхности от скорости ветра
В приведенных примерах при изменении температуры поверхности в рабочем диапазоне коэффициент теплоотдачи изменяется на 5%, влиянием температуры можно пренебречь. Под действием ветра коэффициент теплоотдачи меняется почти в 10 раз.
Коэффициент теплопередачи при увеличении скорости от 0 до 15 м/с увеличивается примерно на 20%. Приведенная в [1] величина коэффициента теплоотдачи на наружной поверхности 35 Вт/м?•°С соответствует скорости ветра около10 м/с (по другим данным 15 м/с). В этой области теплопередача изменяется несущественно. Думаю, следует оставить эту цифру в расчете и не делать соответствующую ячейку доступной для редактирования.
Если пытаться соотнести величину теплопотерь через поверхность кожуха с требованиями [3], то возникает еще одна сложность: не ясно, что принять в качестве характерного размера и характерной температуры? В разных источниках ([3],[5]) предлагаются разные способы вычисления характерного размера поверхности:
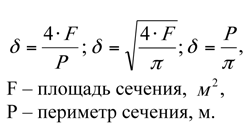
Результаты расчетов по первой и последней формулам для трубопровода Ду100 с изоляцией толщиной 60 мм различаются примерно в полтора раза.
Теплопотери в [3] нормируются в зависимости от размера и температуры внутри
Температура, как по сечению, так и на наружной поверхности, очевидно, неодинакова. Не понятно, применимы ли вообще требования нормативного документа [3] к такой конструкции.
Заключение.
Считаю важной особенностью разбиение поверхности теплообмена по геометрическому признаку. Анализ упрощается, но температурные поля тоже разделяются на области, что в реальности невозможно.
1. Реализованный метод расчета позволяет оценить техническую эффективность спутникового обогрева, может быть использован для экономического анализа.
2. Предложенный метод, будучи доработан и усовершенствован, может применяться для анализа теплопотерь при совместной прокладке трубопроводов в общей изоляции, как это представлено на рисунке 16
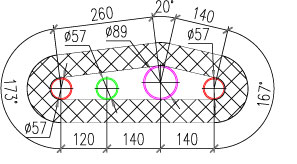
Рисунок 16 – Совместная прокладка трубопроводов в общей изоляции.
3. Количество и допустимая длина спутников определяются теплоотдачей и гидравлическим сопротивлением. Более полное понимание процесса позволит выбрать наиболее правильные режим и параметры обогрева.
Список литературы.
- Хижняков С.В. Практические расчеты тепловой изоляции (для промышленного оборудования и трубопроводов). Изд.3-е, перераб. М., «Энергия», 1976.
- Серия 2.190 – 4м Вводы-выпуски инженерных коммуникаций жилых и общественных зданий для строительства в районах с вечномерзлыми грунтами. Выпуск 1.
- СНиП 41-03-2003 Тепловая изоляция оборудования и трубопроводов.
- СП 41-103-2000 Проектирование тепловой изоляции оборудования и трубопроводов.
- Исаченко В. П.,Осипова В. А.,Сукомел А. С. Теплопередача. Учебник для вузов. — Изд. 3 е, перераб. и доп. М.: Энергия, 1975.













