Умеренная инфляция – необходимое условие практической реализуемости энергосберегающей стратегии

И. Н. Ковалев, доцент Ростовского-на-Дону университета путей сообщения

Уже сложилось понимание того, что для приемлемого отечественного жизнеобеспечения, в частности – качественного развития экономики, нужно незамедлительное, повсеместное и повседневное внедрение энергосбережения, с непрерывным его совершенствованием. К этому обязывает и крайне изношенный парк электростанций, и ограниченные возможности инвестировать как в новые генерирующие мощности, так и в добывающие отрасли углеводородов.

Однако этому препятствует высокая инфляция в стране. Превышение инфляцией некоторого умеренного уровня¹ свидетельствует, прежде всего, об избыточности государственного присутствия в экономике. Но оставив причины возникновения высокой инфляции в стороне, оценим ее влияние на оптимизацию:

• сечений линий электропередач (ЛЭП);
• толщины утепляющего слоя здания;
• мощностей компенсирующих устройств (КУ) и их размещение в энергосистемах.

Проанализируем эти три задачи выбора оптимальных инвестиций на основе минимизации целевой функции приведенных затрат З(l) = К(l)Е_д + C_э (l), где l – параметр строительства, который нужно оптимизировать; К – инвестиции; Е_д – дисконтный коэффициент эффективности, который в условиях рыночной экономики заменяет ранее применяемый в плановой экономике нормативный коэффициент (см. ниже); C_э – стоимости потерь энергии.

Обозначим соответствующие искомые параметры в задачах:

F_j – сечение провода в j-ой линии электропередач;
d_f – толщина утепляющего слоя f-го здания;
Q_ki – мощность КУ в i-м узле сложной сети, например, энергосистемы.

Во всех этих трех задачах эксплуатационные издержки (производственные затраты) сосредоточены в основном в стоимости потерь энергии C_э, в первой и третьей задаче – электроэнергии ∆W, во второй – тепловой энергии ∆V. Без потери общности выводов амортизационные и иные текущие затраты учитывать не будем.

Перечисленные задачи имеют непрерывный характер, когда инвестиции наращиваются небольшими порциями и необходимо определить ту «последнюю порцию»,  которая еще экономически выгодна.

Упомянутый выше дисконтный коэффициент следующим образом выражается через усредненную норму дисконта r будущих доходов от инвестиций и от задаваемого предельного срока окупаемости Т_М  «последней порции» инвестиций [1]:

Е_д = r / [1 – (1 + r)^-Тм]. (1)

Оценка оптимальных сечений ЛЭП

Существует классическая формула для определения экономически оптимального сечения ЛЭП F_э, мм², по критерию dЗ/dl = (dK/dl)) Е_н + dC_э/dl= 0, выражаемая через экономическую плотность тока j_э и максимальный ток линии I:

F_э = I / j_э. (2)

Особенность данной задачи в том, что функция dЗ/dl = 0 в многомерном виде для оптимального расхода металла в сети является сепарабельной, т. е. распадающейся на множество независимых задач, по числу оптимизируемых линий.

Тогда для решения каждой оптимизируемой задачи должно выполняться одно и то же условие оптимума:

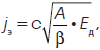(3)

где с – обобщенная константа, определяемая видом материала провода и его физическими показателями;

A – стоимость единицы объема материала провода;

b – стоимость электроэнергии.

Формула (3) образуется минимизацией следующих приведенных затрат, составленных в расчете на одну фазу провода ЛЭП длиной в 1 км:

З = АFE_Д + I²bt (r/F). (4)

Здесь первая составляющая – линейная функция, отражающая затраты на провод, вторая – параболическая, определяемая законом Джоуля - Ленца, который связывает тепловые потери в проводнике с удельным активным сопротивлением r в зависимости от проходящего тока I.

Конкурирующий эффект двух составляющих затрат очевиден: с ростом сечения первая составляющая растет (расход металла на провод), вторая составляющая уменьшается, поскольку с увеличением сечения уменьшается сопротивление и потери электроэнергии (t – время максимальных потерь за год, определяемое формой годовых графиков электрической нагрузки).

В теории электрических сетей показано, что при стоимостных показателях А и b в период конца 1950-х годов, когда цены на углеводороды и электроэнергию были относительно цен на цветные металлы невысокими, экономическая плотность тока для голых алюминиевых проводов находилась на уровне 1 А/мм². В настоящее время ценовой паритет между электроэнергией и металлами сместился в разы в сторону повышения величины b, и эта плотность тока значительно снизилась [2]. Однако данный вопрос выходит за рамками статьи и не влияет на решение поставленных задач.

Будем считать, что отсчет идет от оптимального значения j_Э, найденного при удовлетворительной норме дисконта r = 10 % и при некотором значении заданного срока Т_м окупаемости «последней порции» металла. Нас интересует относительное изменение величины j, а значит и изменение расхода металла и потерь электроэнергии при более высоких нормах дисконта, и соответствующий экономический ущерб, наносимый повышенными инфляцией и определяемой ею нормой дисконта.

Поставим цель оценить указанный ущерб в рассматриваемой и в последующих задачах в относительных единицах и безотносительно цен на те или иные факторы. Диапазон изменения срока окупаемости Т_м примем достаточно широким, например от 3 до 10 лет.

Рассчитаем относительное снижение F* экономического сечения в зависимости от роста нормы дисконта будущих доходов. В качестве базовой величины F_эб примем сечение, определенное при r* = 0,1 и соответствующих значениях Е_д, согласно с (1). На основании (2) и (3) получаем искомое соотношение:

F* = F_v/F_эб = √ (Е_Дб/Е_Дv). (5)

На рис. 1 построены зависимости (5) при изменении дисконта от 10 до 30% при следующих нормируемых значениях Т_м: 5, 8 и 10 лет. Так, при норме дисконта r в 20% и Т_м = 5 лет расход энергосберегающего металла уменьшается на 11%, а при r = 30% – на 20%. При Т_м = 10 лет это снижение возрастает соответственно на 18 и 30%.

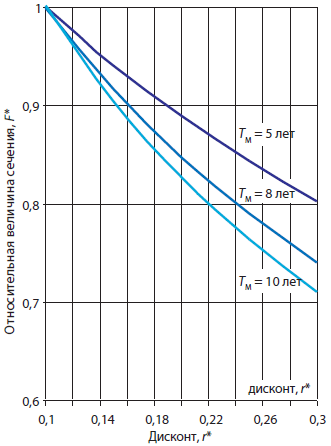Рисунок 1. Снижение энергосберегающих инвестиций в металл при растущих нормах дисконта и нормативных сроков окупаемости

Не имеет смысла сейчас обсуждать, много это или мало в части возникающего ущерба от роста потерь электроэнергии просто потому, что мы рассмотрели только первую составляющую ущерба, от уменьшения инвестиций в энергосберегающий металл.

Но одновременно возникает и второй ущерб – снижаются будущие доходы от увеличения дисконта и при новом, неоптимальном, уменьшенном сечении провода. Возникает вопрос – как просто оценить суммарный, двойной указанный экономический ущерб?

Нетрудно показать, что один из основных рыночных критериев эффективности инвестиций индекс доходности (ИД) определяется формулой из [1]:

ИД = [1 – (1 + r)^-T]/ r • Т₀– 1, (6)

где Т – предполагаемый срок службы линии электропередач;

Т₀ – бездисконтный срок окупаемости инвестиций в целом, равный отношению величины К инвестиций к соответствующей средней величине дохода Д.

Данная формула справедлива и для оценки эффективности инвестиций в их «последнюю порцию», для которой задан срок окупаемости с учетом дисконта Т_М. Определить Т₀ для этой порции по заданной величине Т_М можно, используя известное соотношение из [1]:

Т_М = – [ln(1 - r •Т₀) / ln(1 + r)]. (7)

В результате получим:

Т₀ = [1 – (1+r)^-ТМ]/r. (8)

Однако помним, что найденное значение (8) относится к «последнему слою» провода, а в искомый критерий (6) нужно подставить срок окупаемости всего дополнительного металла, начиная с некоторого базового значения. Здесь нужно использовать известную закономерность для параболической зависимости потерь от тока, а именно: окупаемость инвестиций в целом в два раза короче срока окупаемости «последней порции» металла. Учитывая это, формула (6) в рассматриваемом вопросе имеет вид:

ИД = [1 – (1 + r)^-T] / [1 – (1 + r)^-0.5ТМ] – 1. (9)

Теперь, желая обобщенно оценить снижение ИД из-за роста r, достаточно построить семейство кривых (9) при некотором множестве задаваемых сроков окупаемости Т_м (рис. 2).

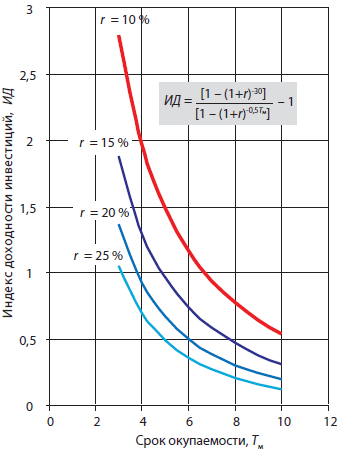Рисунок 2. Снижение рентабельности инвестиций в зави симости от роста нормы дисконта будущих доходов

Построенные зависимости (рис. 2) позволяют сделать вывод, что даже при росте процента с 10 до 15% рентабельность инвестиций в провод линий понижается в 1,5–2 раза. При норме дисконта в 25% ИД сокращается в 3–5 раз.

Таким образом, при современном официальном уровне инфляции и соответствующей норме дисконта в 15–20% рентабельность падает в 2–3 раза. Если же предположить, что реальная инфляция заметно выше 10%, то вложения в чрезвычайно «энергоэффективный» цветной металл становятся, большей частью, нецелесообразными.

Оптимизация толщины утепляющего слоя зданий

В современных ограждающих конструкциях зданий для повышения их тепловой эффективности и снижения расхода теплоты на отопление применяют утеплители с низким коэффициентом теплопроводности l_т. Но стоимость соответствующего материала превышает стоимость обычного строительного материала. Оптимальная (экономически целесообразная) толщина утепляющего слоя d_э не зависит от площади ограждающих конструкций, но определяется соотношением стоимости утеплителя и стоимости сэкономленной за счет его использования энергии. Целевая минимизируемая функция [1] здесь:

З = кdЕ_Д + (t_в – t_н)l_тC_т/d, (10)

где t_в и t_н – температура соответственно внутреннего и внешнего воздуха;
к – удельная стоимость утепляющего слоя;
С_т – стоимость тепловой энергии.

Аналогия целевых функций (4) и (5) делает изложенный выше алгоритм экономического анализа пригодным для данной теплотехнической задачи.

В [1] показано, что

d_э = [(t_в – t_н)lС_т/кE_д]^0.5. (11)

Отсюда следует, что относительное снижение толщины утеплителя в зависимости от роста дисконтной ставки определяется так:

d_э2/d_э1 = (Е_Д1/Е_Д2)^0.5. (12)

Как видим, относительная оптимальная величины утепляющего слоя зависит от нормы дисконта в той же мере, что расход металла в линиях электропередач. Поэтому все сделанные выводы в части влияния процента r на эффективность энергосберегающих мероприятий остаются в силе и в данной задаче.

Важно и то, что аналогия просматривается и в двух других отношениях: во-первых, по масштабности охвата строящихся объектов (ЛЭП напряжением свыше 1000 В и зданий любого предназначения), во-вторых, по виду математической модели оптимизации.

И в том, и в другом случае модель относится к нелинейному математическому программированию с сепарабельной целевой функцией, т. е.распадающейся на множество независимых друг от друга одномерных задач, что и следует из формул (2) и (11).

Проиллюстрируем выводы к рассмотренным двум задачам

Предположим, что согласно (2) и (3), а также (11) при дисконте 10% и Т_м = 5 лет были рассчитаны экономически оптимальные сечения проводов линий электропередач и толщины утеплителей для зданий (базовый вариант, принимаемый за оптимальный).

Примем за единицу соответствующую величину оптимальных инвестиций. Согласно рис. 2 в обоих случаях индекс доходности ИД равен 1,5, т. е. на каждый вложенный рубль в «последнюю порцию» металла и толщины утеплителя уже через 20 лет и более будет получен доход порядка 1,5 руб. (доход от «предыдущих порций» материалы выше, и тем выше, чем ниже лежат эти порции).

Допустим, мы хотим оценить ущерб от того, что дисконт окажется выше заложенного в расчет, например 15, 20, 25%. В табл. 2 показаны показатели базового варианта и остальных трех. Отсюда следует, что энергосберегающие инвестиции К* снижаются на 10–20%, а ИД* соответственно в 1,5–3 раза.

Таблица 1 Оценка экономического ущерба от роста дисконта по сравнению с базовым вариантом

r, % К* ИД* 10 1,00 1,5 15 0,91 1,0 20 0,85 0,7 25 0,79 0,5

Таблица 2 Экономические расчеты КРМ при возрастающей норме дисконта r и Тм = 5 лет

r, % QкΣ, Мвар К, млн руб. δΔW,млн кВт•ч ΔС, млн руб. Т0, лет ДД, млн руб. ИД 5 127 64 12,7 44,4 1,44 461 6,2 10 117 58 12,0 42,2 1,37 321 4,5 15 108 54 11,5 40,6 1,33 237 3,4 20 100 50 11,0 39,0 1,28 182 2,6 25 90 45 10,1 35,9 1,25 139 2,1

Если за базовый вариант принять дисконт в 5% (уровень развитых стран), то ИД резко упадет, по крайней мере, вдвое, т. е. снизится по сравнению с оптимальным вариантом почти в 3–6 раз.

Именно этот ущерб от повышенной инфляции способен полностью подорвать внедрение энергосберегающих технологий, что является главным выводом из проделанного анализа.

Оптимизация мощностей компенсирующих устройств и их размещение в энергосистемах

Данная задача принципиально отличается от первых двух в математическом плане – теперь искомые переменные взаимозависимы, что делает задачу несепарабельной, многомерной и от этого менее обозримой. Но ее масштабность и значимость не уступает рассмотренным выше. А анализируемые сугубо экономические закономерности окажутся практически полностью аналогичны только что выясненным.

Методика экономического анализа будет иной в связи с отмеченной системной спецификой. Здесь будут изучены результаты расчетных экспериментов, проведенные с применением эталонной модели и программы расчета [3].

Физико-техническая суть вопроса компенсации реактивных мощностей энергосистем (КРМ) проста: в отличие от активной электрической мощности потребителя P_i, которая генерируется электростанциями (где на это тратятся первичные энергоносители: органическое или ядерной топливо, энергия падающей воды), отстающая реактивная мощность Q_i может большей частью генерироваться на месте. Это выгодно технически и экономически, поскольку ее передача по сети сопровождается различными потерями: напряжения, активной мощности и электроэнергии.

Кроме того, требуются дополнительные инвестиции в повышение пропускной способности сети. С этой целью поблизости от потребителей электроэнергии устанавливаются дешевые КУ, в основном это батареи силовых конденсаторов. При этом сеть разгружается от потоков реактивной мощности и поэтому снижаются перечисленные потери и затраты.

Пример

Рассмотрим вопрос оптимального выбора мощностей КУ Q_кi в нагрузочных узлах сети напряжением 110 кВ (и выше) реальной энергосистемы Южного Федерального округа.

Исходная технико-экономическая информация:

• схема и параметры электрической сети, активные и реактивные мощности в узлах сети;
• удельная стоимость к_ку = 500 руб./квар.;
• стоимость электроэнергии b = 4 руб./кВт•ч;
• срок службы компенсирующих устройств Т ≥ 15 лет;
• максимальный срок окупаемости инвестиций Т_м = 5 лет.

Оптимизационный расчет проведем для базового режима при r = 5% и для четырех режимов при r = 10, 15, 20 и 25%. Для каждого из этих пяти вариантов расчета определяется суммарная мощность КУ и годовые потери электроэнергии ∆W_с в сети.

В общем виде минимизируемые приведенные затраты определяются как:

З = к_у Q_К∑ Е_д + b∆W_с, (13)

где Q_К∑ – искомая суммарная мощность КУ, которая оптимально распределяется между отдельными i-ми потребителями электроэнергии;

∆W_с – суммарные потери электроэнергии в энергосистеме, зависящие в том числе от протекающих реактивных мощностей Q_i.

В сильно упрощенном виде, но без потери основных свойств задачи, целевую функцию (13) можно представить в виде квадратичной формы [4, 5]:

З = 1^t Q_к к_ку Е_Д + (b t Q_в^t R Q_в)/U², (14)

где 1^t – единичный вектор-столбец, значком t обозначена операция транспонирования;
Q_в = Q – Q_к – вектор-столбец входных реактивных мощностей узлов сети, получаемых за вычетом искомых мощностей КУ;
U – усредненное напряжение сети;
к_ку – удельная стоимость КУ.

Минимум приведенных затрат (13) определяется решением системы уравнений, где каждое уравнение является частной производной по искомой мощности Q_кi:

∂∆W_с/∂Q_кi = – к_у Е_д/b. (15)

Расчетные эксперименты проводились с помощью программно-методического комплекса КРМ-РИИЖТ, получившего в 1990 году лицензию Главгосэнергонадзора на проведение коммерческих расчетов КРМ в энергосистемах [3]. Подробности соответствующих алгоритмов расчета рассмотрены в [3–5].

Схема проведения расчетных экспериментов и экономического анализа

В качестве базового решения оптимизируется выбор мощности и размещение КУ при дисконте r = 5%. и исходных потерях электроэнергии ∆W₀. В процессе расчетов программа каждый раз определяет потери электроэнергии ∆W_f после  размещения очередной партии КУ. Рассчитывая соответствующую разницу потерь электроэнергии d∆W, можно оценивать доходность очередной партии КУ.

После базового расчета проигрываются еще четыре варианта решения задачи КРМ с возрастающей величиной r, с шагом изменения в 5%. И каждый раз определяются снижающиеся суммарные мощности Q_K∑ и соответственно уменьшенные доходы энергокомпании. Результаты сведены в табл. 2.

Обнаруживается практически идентичная картина резкого падения экономической эффективности. Так, суммарная мощность КУ при повышения дисконта с 5 до 25% снижается на 30%, при повышении дисконта с 10 до 20% – снижается на 20%. И соответственно рентабельность инвестиций падает в 3 и 2 раза.

На рис. 3 даются сравнительные инвестиционные потоки (инвестиции К и дисконтированные доходы ДД) для двух вариантов КРМ. Здесь ту же картину можно видеть и так: повышение дисконта с 10 до 20% снижает индекс доходности инвестиций в 2 раза, что также практически совпадает с выводами двух рассмотренных задач.

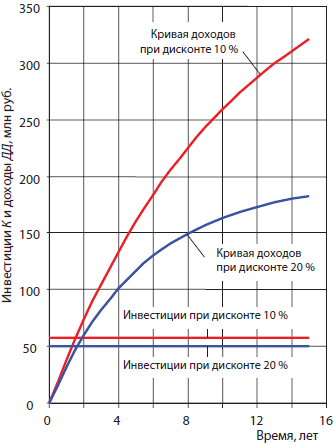Рисунок 3. Инвестиционные потоки процесса КРМ при различных дисконтах

На основании изложенного материала, можно сделать следующие выводы.

1. В сложившихся условиях крайне изношенного парка электростанций и ограниченных инвестиционных возможностей в части расширения добычи углеводородов стратегия энергосбережения представляется единственно возможным вариантом успешного и качественного экономического развития.

2. Необходимым условием реализуемости указанной стратегии является обеспечение нормы дисконта доходов от энергосбережения, не превышающей 10%. Более высокий дисконт снижает рентабельность инвестиций в разы, и в условиях рыночной среды становится своеобразным тромбом на пути энергоэффективного развития.

3. На трех разнохарактерных реальных проблемах энергосбережения выявлена общая закономерность: рост инфляции (а вместе с тем и нормы дисконта) сопровождается двойным ущербом для энергосберегающей политики. Во-первых, существенно снижается уровень целесообразного энергосберегающего инвестирования, ориентированного на определенный срок его окупаемости. Во-вторых, серьезно снижается экономический эффект от эксплуатации оставшихся заниженных инвестиций. В их итоге рентабельность понижается в разы по сравнению с уровнем дисконта в 10%.

Литература

1. Дмитриев А.Н., Ковалев И.Н., Табунщиков Ю.А., Шилкин Н.В. Руководство по оценке эффективности инвестиций в энергосберегающие мероприятия. М. 2005.
2. Ковалев И.Н., Осипов М.А. Об экономически целесообразных плотностях тока в линиях электропередачи энергосистем // Электричество. 1999. № 9.
3. Ковалев И. Н., Репьев В. Г., Самсонова Е. Ю., Теренин М. И. Оптимизация входных реактивных мощностей подстанций энергосистем // Электричество. 1988. № 5.
4. Ковалев И.Н. Метод расчета компенсации переменных электрических нагрузок в электрических сетях // Изв. АН СССР. Энергетика и транспорт. 1973. № 2.
5. Ковалев И.Н. Выбор компенсирующих устройств при проектировании электрических сетей. М. 1990.