Проектирование зданий, благоприятных для жизни

А. В. Волков, Ведущий специалист отдела программной поддержки ЗАО "БЮРО ТЕХНИКИ кондиционирования и охлаждения"

Аннотация

В данном докладе рассматривается способ создания алгоритма для автоматизированного построения математических моделей разветвленных сетей воздуховодов систем вентиляции воздуха.

1. Введение

Согласно данным, полученным Комитетом по охране окружающей среды США (EPA), уровни содержания основных загрязнителей в воздухе внутри жилых помещений, административных и торговых зданий обычно в 2 - 5 раз выше, чем в наружном воздухе. В отдельных случаях это превышение может составлять до 70 раз [1]. Поскольку человек проводит 70 - 98% своей жизни внутри помещений, то можно сказать, что опасность для здоровья человека от воздействия химических веществ внутри здания во много раз увеличивается.

Переносимые воздушными потоками вещества, отрицательно влияющие на качество воздуха внутри помещений, могут быть разделены на две основные категории: газы и взвеси. Основные проблемы для здоровья человека связаны с такими газами как радон, СО, NO₂ и углеводороды. Взвешенные вещества поступают в помещение с табачным дымом, спорами плесени, перхотью животных, спорами растений.

Здание считается "больным", если около 20 % жителей страдают постоянными симптомами заболеваний, которые исчезают, когда люди выходят на улицу. Новые здания обычно более "больны", чем старые из-за уменьшенного воздухообмена, созданного, чтобы сохранить тепло, а также из-за выделения различных химических веществ мебелью и коврами. Современное экономичное строительство, например в России, в соответствии с национальными строительными нормами приводит к тому, что большинство из вновь построенных зданий можно считать "больными".

Самым распространенным методом уменьшения загрязнения воздуха внутри помещений является применение систем вентиляции и кондиционирования воздуха. Однако на пути проектирования таких инженерных систем стоит ряд сложнейших научных и инженерных проблем.

Одной из важнейших задач, возникающих при проектировании систем вентиляции и кондиционирования воздуха, является задача доставки необходимого количества воздуха в нужную зону. Она тем более усложняется, если речь идет о применении централизованных систем с сильно разветвленной сетью воздуховодов.

Неудовлетворительные результаты расчета таких сетей, возникающие при использовании традиционных методов расчета, обусловлены целым рядом допущений, обсуждать которые мы здесь не будем. Их суть хорошо видна при проведении пусконаладочных работ, связанных с регулировкой сети для ее вывода на проектные расходы воздуха. И, увы, как часто эта цель оказывается так и не достижимой. Например, с помощью дополнительных сопротивлений наконец-то добились необходимых соотношений расходов воздуха в ветвях сети воздуховодов, но вдруг заметили, что вследствие их установки и, следовательно, дополнительной нагрузки на вентилятор, снизилось общее количество воздуха в сети. Что делать дальше ? Заказывать, покупать и устанавливать новый, более мощный вентилятор и затем повторить все с начала ?

На наш взгляд, выход из этой ситуации лежит в области предварительного математического моделирования поведения разветвленной сети воздуховодов, замкнутой на конкретные аэродинамические характеристики вентиляторов.

2. Формализованные топологические методы составления математических моделей систем вентиляции воздуха

Разработка формализованных методов составления уравнений математических моделей разветвленных сетей воздуховодов позволяет не только в значительной мере упростить их вывод, но и полностью автоматизировать этот процесс, что является необходимым условием при создании современных комплексов автоматизированного проектирования систем вентиляции воздуха. Решение этого вопроса в равной мере необходимо при создании комплексов профессиональных программ имеющих свой встроенный графических редактор, так и использующих дополнительные возможности внешних графических редакторов, например AutoCAD, которые могут быть направлены для решения прикладных задач имеющих вычислительный характер. Вопрос о том, какой из этих путей лучше, здесь не рассматривается, так как все зависит от соотношения графических и вычислительных трудностей возникающих при решении конкретной задачи.

В данном докладе описывается топологический метод формирования математических моделей разветвленных сетей воздуховодов систем вентиляции воздуха имеющих древовидную структуру.

Сеть воздуховодов может быть представлена в виде совокупности, соединенных между собой, ее отдельных элементов, например, прямолинейных участков воздуховодов, вентиляторов, фильтров и т. п. Этот абстрактный элементарный элемент сети разумнее всего представить в виде четырехполюсника, на входе которого давление и расход воздуха соответственно равны p_H и Q_H, а на выходе - p_K и Q_K.

Рисунок 1. Абстрактный элемент пневматической линии как четырехполюсник

Характеристики (передаточные функции) элементарных элементов сети могут быть заданы различными способами. Так, например, для описания течения воздуха по прямолинейным участкам воздуховодов обычно используются различные типы уравнений, описывающие это течение при определенных условиях с той или иной степенью точности. Характеристики таких элементов как вентиляторы, фильтры, воздухонагреватели обычно задаются с помощью так называемых аэродинамических характеристик, представляющих собой набор необработанных экспериментальных данных, отражающих зависимость потерь давления от расхода воздуха при его течении через элемент. В некоторых случаях характеристика элемента может быть задана полуэмпирическим способом, то есть при использовании значений коэффициентов местных сопротивлений в сочетании с уравнением движения воздуха.

В данной работе, при описании установившегося течения несжимаемого воздуха в абсолютно жестких воздуховодах, принята модель с сосредоточенными параметрами. В этом случае уравнения движения и неразрывности воздуха для j-го элемента сети (участка воздуховода) будут иметь вид

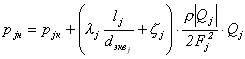 (1)

 (2)

где p_jH и p_jK - давление воздуха в начальном и конечном сечении j-го участка воздуховода, П_a;

Q_jH и Q_jK - расход воздуха соответственно на входе и выходе j-го участка воздуховода, м³/c;

u_j -скорость воздуха в j-ом участке воздуховода;

F_j - площадь проходного сечения j-го участка воздуховода, м²;

l_j - длина j-го участка воздуховода, м;

d_эквj - эквивалентный диаметр j-го участка воздуховода, м;

z_j - коэффициент местного сопротивления j-го участка воздуховода;

r - плотность воздуха, кг/м³;

l_j - коэффициент сопротивления по длине j-го участка воздуховода.

Аэродинамическая характеристика элемента сети может быть определена следующим образом

 (3)

 (4)

Прежде чем перейти к описанию алгоритма формирования математической модели системы вентиляции воздуха сделаем следующие определения.

В качестве участка сети воздуховодов будем подразумевать участок сети с одинаковым расходом воздуха. В общем случае сеть может состоять из участков. В том случае, если такой участок, в свою очередь, состоит из нескольких участков с различной скоростью движения воздуха, он может быть легко сведен к одному эквивалентному.

Под термином воздушная линия будем подразумевать цепочку таких участков направленную от воздухозаборного или воздухораспределительного устройства к вентилятору, который является корнем всей схемы. Количество таких воздушных линий на стороне нагнетания вентилятора обозначим как k_H, а на стороне всасывания - k_В. Тогда общее число воздушных линий в схеме будет

k=k_H+k_В (5)

Внешним узлом схемы будем называть узел, расположенный на ее периферийной части. В нашем случае под этим подразумеваются различные воздухозаборные и воздухораспределительные устройства. Количество внешних узлов схемы равно числу воздушных линий.

Внутренним узлом схемы будем называть узел, соединяющийся с одним предшествующим ему участком схемы (родительским участком) и, по крайней мере, хотя бы с двумя последующими за ним участками (дочерними участками). При этом в качестве направление движения от одного элемента схемы к другому, принято направление от корневого элемента схемы, которым является вентилятор, как в сторону нагнетания, так и в сторону всасывания. Общее число внутренних узлов схемы, имеющей древовидную структуру, определяется соотношением

m=n-k (6)

Рассмотрим алгоритм составления математической модели системы вентиляции воздуха на примере расчетной схемы представленной на рис. 2.

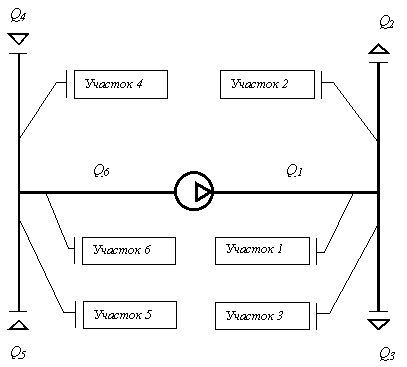Рисунок 2. Пример расчетной схемы системы вентиляции воздуха.

Данная схема состоит из шести участков, то есть n = 6. И имеет на стороне нагнетания и всасывания по две воздушных линии, то есть k_H=2 и k_В=2. В этом случае общее число воздушных линий k=k_H+k_В=2+2=4.

На стороне нагнетания находятся линии 1 и 2. Линия 1 состоит из участков 2 и 1, а линия 2 - из участков 3 и 1. На стороне всасывания находятся линии 3 и 4. Линия 3 состоит из участков 4 и 6, а линия 4 - из участков 5 и 6. Число внешних узлов схемы равно 4, а число внутренних узлов равно 2.

Система уравнений, описывающая движение воздуха на стороне всасывания, состоит из двух уравнений движения и одного уравнения расхода воздуха и может быть записана в следующем виде:

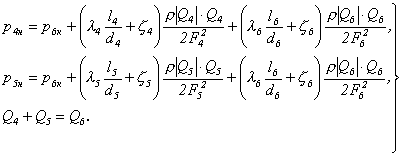 (7)

Уравнения системы (7) могут быть связаны между собой посредством еще оного элемента схемы - вентилятора, аэродинамическая характеристика которого может быть представлена в следующем виде:

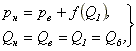> (8)

где p_H и p_B - соответственно давления воздуха на стороне нагнетания и всасывания вентилятора, П_a; Q_H и Q_K - соответственно расходы воздуха на стороне нагнетания и всасывания вентилятора, м³/c.

Обозначим величины давлений воздуха в конце замыкающих элементов сети как

 (9)

и заметим что, в том случае, если воздух забирается из объемов и поступает в объемы с атмосферным давлением, то величины

p₂ = p₃ = p₄ = p₅ = p_a=0.

Таким образом, математическая модель, описывающая движение воздуха в исследуемой системе, может быть записана в виде следующей системы нелинейных алгебраических уравнений

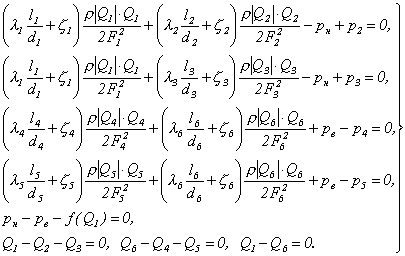 (10)

Данная система состоит из восьми уравнений и содержит восемь неизвестных Q₁, Q₂, Q₃, Q₄, Q₅, Q₆, p_H, p_B и, следовательно, может быть решена относительно этих неизвестных.

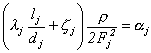 (11)

А теперь попробуем записать систему нелинейных уравнений (10) в матричной форме. Количество строк этой матрицы будет равно количеству уравнений системы (10) и опре со стороны нагнетания вентилятора. Следующие k_B строк - со стороны всасывания. Затем строка, с номером k_H+k_B+1, которая содержит аэродинамическую характеристику вентилятора. На этом, та часть системы уравнений, которая содержит уравнения движения воздуха, заканчивается. А следующие m+1 строк отражают уравнения расходов воздуха. В качестве столбцов этой матрицы будем подразумевать номера участков схемы, при этом 1«i«n+2. Два последних столбца служат для соединения между собой нагнетательной и всасывающей частей схемы.

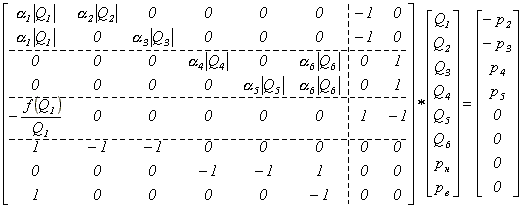 (12)

Обозначим векторы неизвестных и правых частей размерности в выражении (12) как

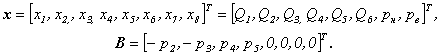 (13)

Тогда матрица соединений A(x)

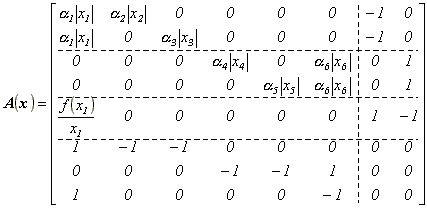 (14)

С учетом обозначений (13) и (14) система уравнений (12) может быть записана в более компактной векторной форме:

 (15)

Следует иметь в виду, что, несмотря на матричную форму записи, система уравнений (15) существенно нелинейна. Это, связано хотя бы с тем, что потери давления воздуха по длине и в местных сопротивлениях воздуховодов могут иметь квадратичный характер. Более того, аэродинамические характеристики многих элементов, таких как вентиляторы, фильтры и т. п., задаются вообще не аналитическим способом. Поэтому, на самом деле, приходиться решать систему нелинейных уравнений. Для этого система уравнений (15) преобразуется к виду:

 (16)

Рассмотренный выше алгоритм может быть полностью автоматизирован, если при формировании схемы в качестве ее элементов использовать структуры представления данных в форме дерева. На рис.3 представлена часть древовидной схемы, на которой изображен j-й участок в сочетании с другими соседними участками. Каждый j-й участок воздуховода имеет указатель на родительский (предыдущий) участок P_j и может иметь указатели на следующий участок N_j и на два дочерних участка C_j⁽¹⁾, C_j⁽²⁾.

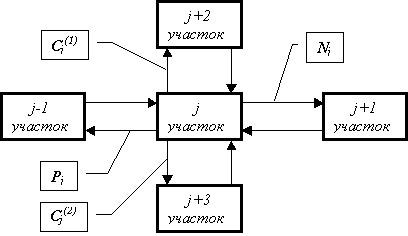Рисунок  3. Структурное представление данных в форме дерева.

Для автоматизированной обработки данных, содержащихся в подобных структурах, удобнее всего применять рекурсивные процедуры и функции, так как не существует однозначно определенных простых способов, позволяющих осуществлять обход элементов этого дерева самым кратчайшим и рациональным способом.

Выводы

Данный алгоритм формирования математической модели разветвленной сети воздуховодов был использован при создании программного обеспечения, позволяющего выполнять аэродинамические расчеты систем вентиляции и кондиционирования воздуха. Сопоставление выполненных расчетов с экспериментальными данными, полученными в ходе выполнения пуско-наладных работ на конкретных объектах, показало, что данный алгоритм качественно верно описывает все возможные процессы, которые могут возникнуть при транспортировке воздуха к потребителю. А в количественном измерении его использование приводит к небольшому превышению потерь давления воздуха в пределах (10-15)% по отношению к экспериментальным данным. Следует особенно отметить, что при использование данного алгоритма можно учитывать такие явления, как превышение или уменьшение давления воздуха (по отношению к атмосферному) в кондиционируемых помещениях, возможность регулирования воздухо-распределительных элементов.