Компьютерное моделирование аэродинамических воздействий на элементы ограждений высотных зданий
Поставленная цель расчета нестационарного вклада от срыва вихрей на периметре здания в распределение ветрового давления по фасадам на интервалах времени, не превосходящих длительность глобальных ветровых порывов в набегающем потоке T0, приводит к следующей постановке задачи.
Компьютерное моделирование аэродинамических воздействий на элементы ограждений высотных зданий
Продолжение. Первую часть статьи читайте в журнале «АВОК», 2006, № 8, с. 18–24.
3. Численное моделирование нестационарного двумерного обтекания профиля здания
Поставленная цель расчета нестационарного вклада от срыва вихрей на периметре здания в распределение ветрового давления по фасадам на интервалах времени, не превосходящих длительность глобальных ветровых порывов в набегающем потоке T0, приводит к следующей постановке задачи.
Двумерное призматическое тело (с сечением, соответствующим контуру здания на заданной высоте) обтекается равномерным изотропным турбулентным потоком несжимаемой среды, имеющим среднюю скорость U, интенсивность турбулентных пульсаций I (определяется как отношение среднеквадратичного значения пульсаций скорости к средней скорости потока в данной точке). В качестве характерных размерных величин берутся скорость U, диаметр тела D, плотность воздуха r. Все физические и геометрические параметры и переменные нормируются на соответствующие комбинации из выбранных характерных величин: линейные размеры – на D, скорости – на U, время t – на D/U, перепады давления – на r U2 и т. д.
Ставится задача рассчитать поле скоростей в потоке, обтекающем здание, и распределение давлений на фасадах здания по периметру горизонтального сечения.
3.1. Математическая модель, расчетная область, технология вычислений
Движение воздушной среды около тела описывается системой уравнений Рейнольдса, замыкаемых с помощью дополнительных дифференциальных соотношений двухпараметрической диссипативной модели турбулентности [10, 11]. Смысл такого подхода состоит в том, что любые мгновенные значения аэродинамических параметров потока представляются в виде суммы осредненной величины и ее пульсационной составляющей. Фактически это означает, что аэродинамическая величина, например, скорость потока, является случайной, осреднение которой во времени дает ее математическое ожидание, а пульсационная составляющая которой – дисперсия случайной величины.
Турбулентное движение всегда имеет все три компоненты скорости, даже если у средней скорости есть только две составляющие. Таким образом, наряду с обычными параметрами потока (осредненная скорость, давление) появляются дополнительные параметры, связанные с характеристиками турбулентных пульсаций. В результате система основных уравнений движения потока воздуха оказывается незамкнутой. Замыкание осуществляется путем привлечения дополнительных уравнений, управляющих законами развития турбулентности.
Существует большое разнообразие моделей турбулентности и, соответственно, способов замыкания системы уравнений турбулентного движения воздушного потока, обзор этих моделей и примеры тестирования можно найти в [10, 16]. Понятие «модель турбулентности» подразумевает совокупность дополнительных уравнений и эмпирических соотношений, замыкающих математическую задачу расчета течений.
В настоящей работе расчеты выполнены с использованием стандартной версии, так называемой «высокорейнольдсовой модели k-e» [11] (k – удельная кинетическая энергия турбулентных пульсаций, k = 3 I2/2, e – скорость диссипации турбулентной энергии, связанная с масштабом турбулентности L по формуле eL = Ck 3/2, C = 0,164). Используется вычислительная технология пакета STAR-CD (метод контрольного объема, интерполяция конвективных членов по схеме QUICK, неявная схема шагов по времени, внутренний итерационный алгоритм PISO) [11].
Требование проведения расчетов при различных направлениях набегающего ветрового потока влечет необходимость поворота исследуемого профиля здания. Для этого в сетку вмонтирован промежуточный цилиндрический эле-мент (рис. 4), позволяющий круговым смещением расчетных узлов в необходимом направлении получать новую расчетную сетку с задаваемым углом поворота профиля здания по отношению к направлению набегающего потока.
 |
Рисунок 4. В сетку вмонтирован промежуточный цилиндрический элемент, позволяющий круговым смещением расчетных узлов в необходимом направлении получать новую расчетную сетку с задаваемым углом поворота профиля здания по отношению к направлению набегающего потока |
Поскольку вниз по потоку от тела распространяются нестационарные вихревые структуры, возникающие при отрывах на острых кромках профиля, сетка в области III выполнена с достаточным для разрешения этих структур измельчением (рис. 5).
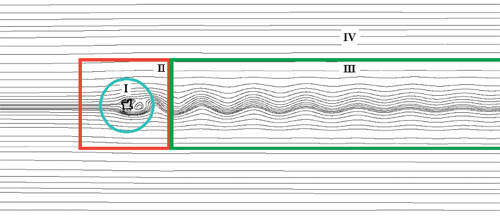 |
Рисунок 5. Поскольку вниз по потоку от тела распространяются нестационарные вихревые структуры, возникающие при отрывах на острых кромках профиля, сетка в области III выполнена с достаточным для разрешения этих структур измельчением |
Размер ячеек в пристеночной области I составляет 0,007 D, в области IV – 0,3 D, в дальнем следе за телом (в области III) – 0,1 D. Общее количество контрольных объемов – 102 000.
Начальные условия: покоящаяся среда.
Граничные условия:
• на входе в расчетную область задается скорость потока U, интенсивность турбулентных пульсаций I и масштаб турбулентности L (в большинстве случаев принималось L = 0,1 D, I = 1 %, U = 10–30 м/с);
• на выходе – условие постоянства давления p = p∞;
• на удаленных внешних боковых границах – условие аэродинамически гладкой стенки (вектор скорости параллелен боковой границе расчетной области);
• на внутренней границе (на периметре здания) – условие прилипания (нулевая скорость), со сшивкой профилей скорости при помощи пристеночных функций, основанных на так называемом «законе стенки» [10, 11, 16].
После выхода на квазипериодический режим изменения по времени интегральных аэродинамических коэффициентов продольной и поперечной составляющих аэродинамической силы решение считается оконченным. Для более точного воспроизведения нестационарных эффектов проводятся дополнительные расчеты с меньшим шагом по времени на интервале в три основных периода.
Результатом расчета являются картины обтекания и распределения Ср = ƒ(N, t) по периметру здания. По ним находятся средние и пульсационные характеристики ветровых нагрузок.
3.2. Результаты численного моделирования
Расчеты нестационарного обтекания профиля здания (рис. 1) выполнены для четырех основных и четырех промежуточных румбов ветра в диапазоне U = 10–30 м/с.
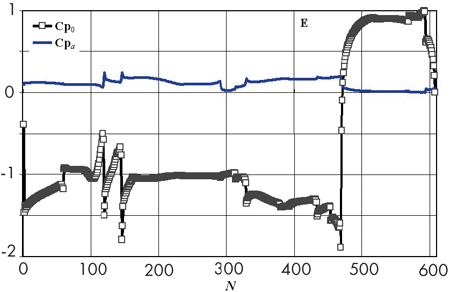
На рис. 6 приведены распределения средних значений Cp0 и амплитуды пульсаций Cpa по периметру здания для восточного и северо-западного румбов ветра. По оси абсцисс отложены условные номера N = 1 – 608 характерных точек на периметре горизонтального сечения здания (схема расположения этих точек на фасадах соответствует рис. 1в, 11). В исследованном диапазоне скоростей ветра эти распределения оказались практически универсальными, что является отражением свойства автомодельности среднего течения по числу Рейнольдса для профиля здания рассмотренной конфигурации.
 |
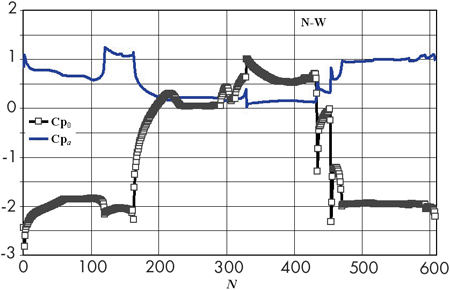 |
Рисунок 6. Распределение средних значений Cp0 и амплитуды пульсаций Cpa по периметру здания для восточного и северо-западного румбов ветра. По оси абсцисс отложены условные номера N = 1 – 608 характерных точек на периметре горизонтального сечения здания (схема расположения этих точек на фасадах соответствует рис. 1в, 11) |
На рис. 7 показан пример расчета картины мгновенного поля скоростей около профиля здания (направление ветра в данном случае восточное). Первичный отрыв потока происходит сразу же на лобовых (передних) острых кромках, в результате почти все фасады постоянно находятся в зоне возвратно-циркуляционного течения. Некоторые из циркуляционных областей являются устойчивыми и не изменяются во времени. К таким можно отнести стационарный вихрь, локализующийся в углублении профиля на лобовой поверхности, и два квазиустановившихся вихря в южной части рассматриваемого контура. В северной и западной частях профиля обтекание нестационарное, с изменяющимся направлением потока вдоль контура здания из-за поочередного срыва вихрей с его угловых кромок. Этот процесс сопровождается возникновением значительных пульсаций давления на подветренных и боковых фасадах (рис. 6а).
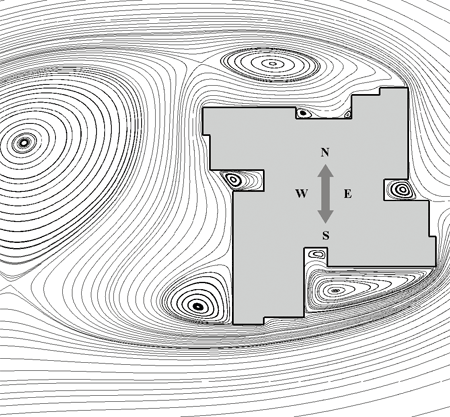 |
Рисунок 7. Пример расчета картины мгновенных линий тока около профиля здания (направление ветра в данном случае восточное) |
Зоны наиболее интенсивного ветрового отсоса находятся, главным образом, в окрестности угловых кромок фасадов, где зарождаются отрывные области (рис. 7). В этих же местах наблюдаются наиболее высокие амплитуды колебаний давления и, как следствие, возникновение высоких пиковых нагрузок (рис. 6). Также следует отметить, что для промежуточных направлений ветра величина пульсационной составляющей давления существенно выше, чем для основных направлений (запад, север, восток, юг).
| Таблица 2 Результаты вычисления средних по времени значений интегральных аэродинамических коэффициентов при различных румбах ветра |
||||||||||||||||||||||||||||||||||||
|
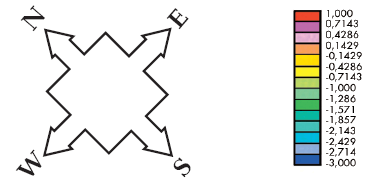
На рис. 8 для примера приведены мгновенные картины распределения Cp в пространстве вблизи здания при северо-западном ветре в последовательные моменты времени на периоде колебаний. Для представления результатов использована система координат, в которой ось абсцисс ориентирована по направлению ветра слева направо, а здание повернуто в зависимости от выбранного румба. Переменная времени t нормирована на t0 = D/U, т. е. представлена в безразмерном виде – в долях от t0. Наличие сильно выступающих вперед и в стороны (по отношению к направлению ветра) острых кромок фасадов приводит в данном случае к возникновению интенсивных колебаний ветрового отсоса, вызванных попеременным сходом с этих кромок крупных вихрей (рис. 8). Амплитуда пульсационной составляющей коэффициента Cp может достигать 50 % от среднего значения Cp0 (рис. 6б).
Аналогичные картины течения (с некоторыми различиями в деталях) характерны для всех рассмотренных направлений обтекания контура данного здания.
 |
 |
a) t = 1,5 |
б) t = 3 |
 |
 |
в) t = 4,5 |
г) t = 6 |
 |
|
Рисунок 8. Мгновенные картины распределения Cp в пространстве вблизи здания при северо-западном ветре в последовательные моменты времени на периоде колебаний |
|
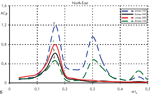
На рис. 9 даны примеры расчета спектра пульсаций коэффициента давления Cp для характерных угловых точек фасадов при восточном и северо-восточном направлениях ветра (по оси абсцисс отложена безразмерная частота wt0; t0 = D/U).
Наряду с основной частотой, при которой наблюдаются максимальные амплитуды, в ряде случаев, что особенно выражено при промежуточных румбах ветра, существенными оказываются вторые гармоники, вызванные вторичным образованием крупных вихрей на выступах здания (рис. 9б). Главным образом, области с двухчастотным спектром находятся в донной области в окрестности кромок, на которые поочередно набегает то левый, то правый оторвавшийся вверх по потоку вихрь. Размер и интенсивность схода этих вихрей неодинаковы, что приводит к сдвигу их воздействия во времени.
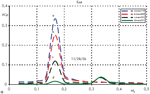 |
Рисунок 9а (подробнее) Рисунок 9б (подробнее)
Примеры расчета спектра пульсаций коэффициента давления Cp для характерных угловых точек фасадов при восточном и северо-восточном направлениях ветра (по оси абсцисс отложена безразмерная частота wt0 ; t0 = D/U) |
 |
| Таблица 3 Сравнение результатов расчетов максимального ветрового отсоса на фасадах здания по методу СНиП [2] и по предлагаемой гибридной методике (для типа местности «C» при v = 0,9) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Числа Струхаля (12), вычисленные по основной частоте колебаний местных ветровых нагрузок, лежат в диапазоне 0,135 < Sh < 0,165. В ряде зон фасадов, в зависимости от направления ветра, могут возникать значительные колебания на двойной и тройной частоте (рис. 9б).
В табл. 2 даны результаты вычисления средних по времени значений интегральных аэродинамических коэффициентов при различных румбах ветра. Увеличение абсолютных значений коэффициентов cx0, cу0 для промежуточных румбов объясняется увеличением фактического поперечного размера обтекаемого контура примерно в 1,4 раза (все коэффициенты отнесены к одному и тому же размеру D и к единице высоты здания).
Наряду с аэродинамическим воздействием в направлении ветра наблюдаются значительные нагрузки поперек ветра. Главная частота колебаний этих нагрузок соответствует числу Струхаля Sh ≈ 0,15.
4. Расчет ветровых нагрузок по гибридной методике
В результате численного моделирования для каждой точки периметра горизонтального сечения здания (1 ≤ N ≤ 608) были определены зависимости от времени коэффициента давления Cp при всех 8 основных и промежуточных румбах ветрового потока (0° ≤ b ≤ 360°):
Cp = ƒ (t, b, N). (15)
По этим данным вычислено среднее значение
![]() (16)
(16)
и амплитуда
Cpa = ƒ (b, N) (17)
пульсационной составляющей C’p(t) = Cp – Cp0, появляющейся из-за срыва вихрей в окрестности угловых кромок фасадов.
Величины (16), (17) были использованы для вычисления обобщенных распределений абсолютных максимумов среднего и пикового значений коэффициента ветрового отсоса для всех румбов ветра:
![]() (18)
(18)
![]() (19)
(19)
На рис. 10 показано расположение на фасадах зон I умеренного и зон II повышенного среднего и пикового ветрового отсоса (зоны II выделены на рис. 11 рамками). В зонах II максимальное среднее C0 превышает 2,0, а пиковое значение C1 может быть больше 3,0 (рис. 10). Как и следовало ожидать, зоны максимального ветрового отсоса располагаются в окрестности выступающих угловых точек контура здания (рис. 11).
Для любой точки периметра рассмотренного здания существует направление ветра, при котором среднее значение коэффициента ветрового отсоса (–Cp) может превышать уровень 1,7, а пиковое значение – величину 2,6.
Наибольший ветровой отсос (с пиковым значением –Cp до 3–3,5) может быть на фасадах между точками №№ 119–163 и в окрестности угловых точек №№ 1, 329, 469 (рис. 10, 11).
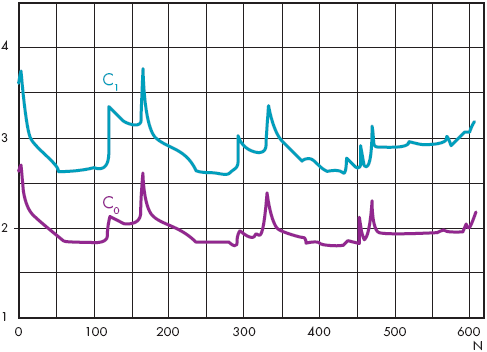 |
Рисунок 10. Распределение по периметру фасадов максимально возможных значений коэффициентов среднего Ср и пикового С1 ветрового отсоса при варьировании направления ветра от 0° до 360° |
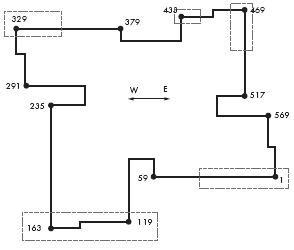 |
Рисунок 11. Зоны максимального ветрового отсоса располагаются в окрестности выступающих угловых точек контура здания (зоны II выделены рамками) |
В табл. 3 дается сравнение результатов расчетов максимального ветрового отсоса на фасадах здания по методу СНиП [2] и по предлагаемой гибридной методике (для типа местности «C» при n = 0,9). Обозначено:
z – высота над уровнем земли, м;
Um – средняя скорость ветра на высоте z, по формулам (2), (5б), м/с;
V – пиковое значение скорости в порыве ветра на высоте z, по формуле (10) при n = 0,9, м/с;
wm – среднее значение максимального ветрового отсоса в соответствии с методикой СНиП, по формуле (4) при c = –2, Па;
w – пиковое значение максимального ветрового отсоса в соответствии с методикой СНиП, по формуле (7), Па;
wmI,II – диапазоны изменения среднего значения максимального ветрового отсоса в зонах I–II, вычисляется при Cp = C0 по формулам (13), (2), (5б), (18) и результатам численных расчетов Cр0 (рис. 10), Па;
(wm + wp0)I,II – диапазоны изменения суммарного пикового значения ветрового отсоса в зонах I–II без учета вторичных пульсаций, связанных со срывом вихрей; вычисляется при Cp = C0 по формулам (14), (10), (5б), (8б), (18) и результатам чис-ленных расчетов Cр0 (рис. 10), Па;
(wm + wp0 + wp1)I,II – диапазоны изменения суммарного пикового значения ветрового отсоса в зонах I–II с учетом пульсаций ветра и вторичных пульсаций, связанных со срывом вихрей; вычисляется при Cp = C1 по формулам (14), (10), (5б), (8б), (19) и результатам численных расчетов Cр0, Cра (рис. 10), Па.
В табл. 4 указаны диапазоны изменения главных частот колебания ветровой нагрузки, связанных со сходом вихрей с профиля здания.
| Таблица 4 Главные частоты колебания ветровой нагрузки, связанные со сходом вихрей на профиле здания |
||||||||||
|
5. Заключение
Предложена гибридная методика проведения расчетов местных ветровых нагрузок на высотное здание, сочетающая традиционные инженерные подходы с возможностями современных методов компьютерного моделирования на основе экономичных двумерных нестационарных моделей турбулентного обтекания.
Дополнительно учтены вторичные пульсации ветровой нагрузки, возникающие из-за образования и срыва крупных вихрей при обтекании «плохообтекаемого» контура здания.
На конкретном примере численного исследования нестационарного обтекания профиля здания найдены распределения средней и пиковой нагрузок по поверхности фасадов при различных направлениях ветра и определены характерные частоты колебаний ветровой нагрузки за счет образования крупных вихрей при обтекании профиля. Определены координаты зон на периметре профиля здания, в которых наблюдается максимальный ветровой отсос. Пиковые нагрузки реализуются в окрестности углов здания. Наряду с аэродинамическим воздействием в направлении ветра, наблюдаются значительные переменные нагрузки поперек ветра.
Результаты сопоставлены с требованиями СНиП 2.01.07-85* «Нагрузки и воздействия». Показано, что пиковые значения местного ветрового отсоса могут на 50–100 % превышать данные, полученные в соответствии с рекомендациями СНиП (без учета коэффициента надежности Vf = 1,4). Расчеты проводились с учетом особенностей фасадной системы строящегося здания и не могут быть непосредственно перенесены на другие объекты.
Для определения нестационарных ветровых нагрузок на здание в целом необходимо проводить расчеты по трехмерным моделям обтекания.
Список литературы, использованной в данной статье, см. в журнале «АВОК», № 8, 2006, с. 24.
Тел. (495) 482-40-58
В статье использовались материалы фирмы «Набад».

Статья опубликована в журнале “АВОК” за №1'2007
Статьи по теме
- Компьютерное моделирование аэродинамических воздействий на элементы ограждений высотных зданий
АВОК №8'2006 - Воздушный режим высотного жилого здания в течение года Часть 1. Воздушный режим при естественной вытяжной вентиляции
АВОК №8'2004 - Многофункциональный высотный комплекс в Москве на Мосфильмовской улице
АВОК №8'2006 - Способы увеличения аэродинамической эффективности вентиляционных систем
АВОК №5'2009 - Противодымная защиты высотных зданий
АВОК №8'2004 - Расчет разности давлений воздуха на наружной и внутренней поверхностях ограждающих конструкций высотных зданий
АВОК №3'2021 - Водоснабжение и водоотведение высотных зданий
Сантехника №6'2004 - Инженерные решения высотных жилых комплексов
АВОК №5'2007 - Теплоаккумуляционные системы отопления и охлаждения помещений офисных зданий
АВОК №2'2012 - Возможность естественной вентиляции для высотных зданий
АВОК №1'2005
Подписка на журналы
















