Еще раз о расчете воздушных завес
Тепло- и массообмен в проеме определяется не геометрическими построениями траектории оси или границ струи, а законами сохранения массы, теплоты и количества движения в зоне проема. Принципиальным условием является соблюдение закона импульса в зоне проема, включающего наружные ограждения".
Еще раз о расчете воздушных завес
В порядке обсуждения нашей статьи "К вопросу о расчете воздушных завес", напечатанной в журнале "АВОК", 2003, № 7, была опубликована статья А. С. Стронгина и М. В. Никулина [2], в которой приведены возражения и сомнения в предпосылках и методах расчета, изложенных в [1]. Мы благодарны оппонентам за внимание к затронутой теме и за сделанные замечания, которые заставили нас более внимательно изучить экспериментальное обоснование ранее использовавшихся методов расчета воздушных завес. Следует признать, что в таблице 3 [1] допущены опечатки - следует читать в третьей строке "ширина щели, мм - 100; скорость воздуха на выходе из щели, м/с - 9,15". Остальные замечания и возражения заслуживают более подробного рассмотрения. Поэтому мы обратились в редакцию журнала "АВОК" с просьбой опубликовать результаты этого рассмотрения.
Теоретическая обоснованность предложенного метода
По мнению авторов [2], "струя воздушной завесы не является аналогом свободной струи, поэтому задание средней скорости на участке разворота и взаимодействия с ограждением (или встречной струей при двухсторонней завесе) не характеризует реальную картину течения. Тепло- и массообмен в проеме определяется не геометрическими построениями траектории оси или границ струи, а законами сохранения массы, теплоты и количества движения в зоне проема. Принципиальным условием является соблюдение закона импульса в зоне проема, включающего наружные ограждения".
Действительно, струя воздушной завесы не является аналогом свободной струи. Попытки упомянутых оппонентами авторов определять траекторию струи без учета поперечного градиента давления, образующегося в искривленной струе, приводили к неудовлетворительным результатам. Только относительно недавно появились работы, достаточно полно учитывающие особенности течения струй в поперечном потоке. В предложенном нами методе [1] определение траектории струи и основных параметров завесы базируется на решении дифференциальных уравнений сохранения энергии и импульса [4].
Теоретическая обоснованность метода В. М. Эльтермана
А. С. Стронгин и М. В. Никулин считают, что по методу, предложенному В. М. Эльтерманом [3] (далее метод В. М. Эльтермана), параметры завесы, обеспечивающей требуемую защиту проема, определяются только на основании решения закона сохранения импульса в зоне проема, включающего наружные ограждения. Обратимся непосредственно к работе В. М. Эльтермана [3]. Там говорится, что решение исходных уравнений сохранения количества масс (уравнение 1) и количества энергии (уравнение 2) сделано "для рационально устроенных воздушных завес" (с. 11). "Рациональным устройство завесы будет тогда, когда струя завесы полностью тормозится силой разности давления (т. е. теряет скорость в направлении оси X) и участок контрольной поверхности НАБВ (рис. 7) не пересекают потоки, выходящие из объема, ограниченного этой поверхностью, наружу" (с. 11, 12). Как видно из приведенных выдержек, геометрические построения траектории и границ струи (рис. 7 [3]) в дополнение уравнениям количества масс и количества энергии потребовались. Более того, при рассмотрении теплового баланса в проеме ворот указывается: "При выводе формулы (37) учитывалось также то обстоятельство, что когда ось струи воздушной завесы пересекает плоскость ворот у верхней кромки, в ворота проходит половина объема воздуха, подаваемого в завесу…" (с. 35). Одновременно В. М. Эльтерман указывает (с. 13): "Как показали опыты, оба указанных выше требования к рациональному устройству завес хорошо выполняются, когда выпуск воздуха производится в плоскости ворот и величина q меньше предельной, указанной в табл. 1".
Следовательно, проверка "рациональности устройства завес" осуществляется все-таки по прохождению траектории струи и может быть заменена некоторыми численными ограничениями на основании тех или иных опытных данных. Отметим, что в табл. 1 имеются значения q > 1. Рассмотрим более подробно основополагающие уравнения 1 и 2 по [3].
Уравнение 1:
Gпр = Gн + Gз,
где Gпр - количество воздуха, проходящее через проем;
Gн - количество наружного воздуха, проходящее через проем;
Gз - количество воздуха, поданного в завесу. Разделив обе
части этого уравнения на Gпр, получим:
1 = Gн/Gпр + q,
где q = Gз/Gпр.
Поскольку для "рационально устроенных завес" наружный воздух не может уменьшать
количество воздуха, проходящее через проем, Gн/Gпр > 0,
но тогда q ![]() 1.
Однако в табл. 1 приведены значения q, существенно большие 1. Это обстоятельство
порождает значительные сомнения в том, что "…оба указанных выше требования
к рациональному устройству завес хорошо выполняются, когда выпуск воздуха производится
в плоскости ворот и величина q меньше предельной, указанной в табл. 1".
1.
Однако в табл. 1 приведены значения q, существенно большие 1. Это обстоятельство
порождает значительные сомнения в том, что "…оба указанных выше требования
к рациональному устройству завес хорошо выполняются, когда выпуск воздуха производится
в плоскости ворот и величина q меньше предельной, указанной в табл. 1".
Уравнение 2:
![]() ,
,
где Fв - площадь ворот;
Fщ - суммарная площадь щелей, через которые выходит струя
воздушной завесы;
F - площадь плоскости АБ;
![]() -
коэффициент расхода воздуха через ворота, защищенные завесой;
-
коэффициент расхода воздуха через ворота, защищенные завесой;
![]() -
поправочный коэффициент на количество движения, учитывающий неравномерность
поля скоростей;
-
поправочный коэффициент на количество движения, учитывающий неравномерность
поля скоростей;
vсж - средняя скорость движения воздуха в сжатом сечении за воротами;
vз - скорость выхода воздуха из щели воздушной завесы;
![]() -
плотность воздуха, выходящего из завесы; .см - плотность воздуха при температуре
смеси воздуха завесы и наружного воздуха;
-
плотность воздуха, выходящего из завесы; .см - плотность воздуха при температуре
смеси воздуха завесы и наружного воздуха;
Rс - среднее реактивное давление стены в пределах плоскостей ВГ
и МН;
![]() -
угол между направлением выхода струи завесы и плоскостью ворот;
-
угол между направлением выхода струи завесы и плоскостью ворот;
![]() -
угол между направлением скорости vсж и осью X (рис. 7а).
-
угол между направлением скорости vсж и осью X (рис. 7а).
В левой части уравнения два слагаемых, первое из которых - проекция на ось Х количества движения потока воздуха, проходящего через проем; второе - проекция на ось Х количества движения потока воздуха, подаваемого в завесу. В первом слагаемом присутствует коэффициент µ - "коэффициент расхода воздуха через ворота, защищенные завесой". Обычно этот коэффициент определяют из решения уравнений сохранения энергии и количества движения, но в сами эти уравнения коэффициент расхода не входит. Введение коэффициента расхода в уравнение количества движения приводит к тому, что количество движения потока воздуха, проходящего через проем, изменяется по непонятной причине кратно величине µ. Очевидно, что баланс количества движения нарушен.
| Таблица 1 [3] | ||||||||||||||||||||||||
|
||||||||||||||||||||||||
Кроме того, второе слагаемое левой части уравнения 2, которое по физической картине течения должно вычитаться из первого слагаемого - "знак минус показывает, что проекция скорости направлена навстречу оси Х" (с. 7 [3]), в уравнении 2 складывается. Указанные обстоятельства позволяют считать уравнения, определяющие взаимосвязь относительного расхода q, коэффициента расхода µ, отношения площадей щели завесы и ворот, угла между направлением выхода струи завесы и плоскостью ворот, полученные в результате решения уравнения 2, необоснованными.
При усовершенствовании метода В. М. Эльтермана [5, 6] предлагается учитывать распределение температуры в поперечном сечении струи и определять точку поперечного сечения, в которой расход струи делится между помещением и наружной атмосферой. Далее предполагается, что указанная точка всегда имеется (струя всегда достигает ограждения проема) и определяется относительным расходом завесы q = Gз/Gпр и относительной длиной струи до ее соприкосновения с ограждением проема f = Fпр/Fщ. Значения q и f предварительно задаются (в [7] рекомендуется принимать q = 0,5-0,6; f = 20-30), затем определяют температуру воздуха на выходе из щели, расход и скорость воздуха на выходе из щели и проводят оптимизацию воздушной завесы по критерию приведенных затрат. При этом А. С. Стронгин и М. В. Никулин [2] считают, что "…в том числе оптимальным может быть случай, когда в проем ворот входит только начальный расход завесы (без присоединения наружного воздуха)". Следовательно, по мнению наших оппонентов, во всем диапазоне значений q и f траектория струи такова, что имеется точка поперечного сечения, в которой струя соприкасается с ограждением проема, и длина траектории струи зависит только от величины угла между направлением выхода воздуха из щели и плоскостью проема без учета искривления траектории под действием поперечного потока.
"Для оптимальных значений угла выпуска воздуха (![]() =
30 °) длина траектории составляет хА = 1,05f"
[5]. Без учета искривления длина траектории составляет
=
30 °) длина траектории составляет хА = 1,05f"
[5]. Без учета искривления длина траектории составляет ![]() .
(В качестве справки укажем, что 1/cos 30 ° = 1,155.)
.
(В качестве справки укажем, что 1/cos 30 ° = 1,155.)
При этом проверка правильности выбора завесы не производится. В свете высказанного странными выглядят замечания в наш адрес: "Достаточным условием обеспечения шиберирующих свойств не является прохождение наружной границы струи через определенную точку…" [2].
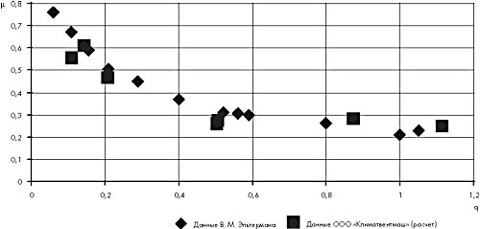 |
Рисунок 1. Зависимость коэффициента расхода µ от коэффициента отношения
расходов q (f=30, |
Об экспериментальной проверке метода В. М. Эльтермана и предложенного метода
Подтверждение справедливости метода В. М. Эльтермана заключается в сопоставлении полученной теоретической зависимости µ = F(q) с экспериментальными данными: "…расчетные значения, определенные по формуле 9, хорошо совпадают с опытными (см. § 3)" (с. 13 [3]). Но, как было показано выше, теоретические зависимости не имеют физической основы.
Поэтому сопоставление экспериментальных данных с ними не может служить подтверждением правильности теории. Из описания условий эксперимента видно, что проверка условий "рационально устроенных завес" проводилась только на соответствие значений q предельным значениям из табл. 1. Не проверялось и соблюдение уравнения 1.
Представленные выше результаты рассмотрения метода В. М. Эльтермана побудили к разработке альтернативного метода расчета воздушных завес.
На основании математической модели, позволяющей строить траекторию струи
завесы, мы численно провели эксперимент, аналогичный описанному в [3] для двухсторонней
завесы с f = 30, углом между направлением выхода воздуха из щели завесы
и плоскостью проема ![]() =
45 °, µ 0 = 0,8. В зависимости от расположения струи завесы
относительно проема рассматривались два случая:
=
45 °, µ 0 = 0,8. В зависимости от расположения струи завесы
относительно проема рассматривались два случая:
1. Струя завесы не достигает дальней стенки проема.
2. Струя завесы достигает дальней стенки проема и разделяется на две части,
одна из которых (внутренняя) попадает в проем.
В первом случае расход воздуха через проем равен сумме расхода струи завесы и расхода наружного воздуха, врывающегося вместе со струей. Этот расход вычислялся как произведение площади проема, не перекрытой струей, на скорость воздуха в проеме. Скорость воздуха в проеме определялась по заданному перепаду давления на проеме и коэффициенту расхода свободного проема.
Во втором случае расход воздуха через проем вычислялся аналогично тому, как это сделано в [8].
Полученные в результате значения µ и q нанесены на график из [3], приведенный также в [2] (рис.1). качественно и в достаточной степени количественно коррелируются с экспериментальными данными [3].
Следует отметить, что при численном моделировании нами установлено, что в рассматриваемом случае точка q = 0,5, µ = 0,246 соответствует режиму, когда струя завесы перекрывает проем и не вырывается наружу. Исследование экспериментальных данных Г. Т. Татарчук [9] показало, что призначении µ = 0,24-0,25 также имеет место стабилизация значения µ (рис. 2 [9]).
Кроме того, в случае когда струя завесы перекрывает проем и не вырывается наружу, потери тепла с частью струи, уходящей наружу Q0, должны быть равны 0.
На основании рис. 5 [9] мы построили зависимость значений q0, которым соответствует значение Q0 = 0 (рис. 2).
Там же нанесены значения q0, вычисленные нами на основании вышеуказанной
математической модели. При моделировании опытов Г. Т. Татарчук µ0 =
0,64 и ![]() =
30°.
=
30°.
Из рис. 2 видно, что наши данные качественно коррелируются с экспериментальными данными [9]. <,br> Мы приводим эти данные для того чтобы показать, что математическая модель течения струи завесы, основанная на теории течения струи в поперечном потоке, позволяет получать результаты, сопоставимые с экспериментальными данными.
Приведенные в [1] расчетные траектории завес иллюстрируют их сопоставимость с теплограммами по расположению траектории струи относительно проема.
Средняя температура воздуха в сечении, соответствующем концу струи, определялась по распределению температуры в сечении. Автору работы [5] должно быть понятно, что при известных (из теплограммы) температурах на оси и по границам струи можно определить среднюю по сечению температуру. Относительно замечаний по табл. 4.2 [1] следует отметить, что из рис. 2 видно, что 3,5 м - это размер вдоль струи (завеса верхняя). Поэтому скорость выпуска нужно считать при длине щели 1,5 м.
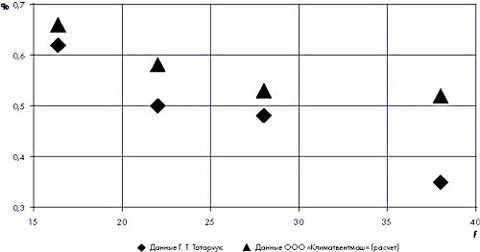 |
Рисунок 2. Зависимость отношения расходов воздуха через щель завесы и черзе проем при нулевых тепловых потерих струи, q0, отношения проходных сечений проема и щели завесы, f |
Заключение
Наш подход к подбору воздушных завес строится на следующих факторах.
При рационально выполненной завесе сквозь проем проходит только струя завесы. При этом температура воздуха, проходящего через проем, даже в случае прохождения части струи вне проема, будет не ниже значения средней температуры в сечении струи, первым соприкасающимся с ограждением проема. Поэтому мы не определяли среднюю температуру части струи, попадающей в проем в случае разделения струи, хотя такая возможность имеется. Для проверки выполнения в выбранной завесе условия перекрытия проема строится траектория струи этой завесы, что дает возможность оценить расположение струи относительно проема и принять решение о пригодности выбранной завесы. Задание значения средней скорости воздуха в сечении струи, первым соприкасающимся с ограждением проема (средняя скорость в конце струи), или, что более точно, соотношения средней скорости и скорости в проеме ворот без завесы, позволяет при подборе завесы определить условия формирования траектории струи при воздействии поперечного потока.
В заключение мы обращаемся ко всем заинтересованным лицам с просьбой сообщать нам любые сведения о натурных испытаниях завес, что позволит нам проверять и совершенствовать метод расчета воздушных завес.
Литература
1. Дискин М. Е. К вопросу о расчете воздушных завес // АВОК. 2003. № 7.
2. Стронгин А. С., Никулин М. В. К вопросу о расчете воздушно-тепловых завес // АВОК. 2004. № 1.
3. Эльтерман В. М. Воздушные завесы. М.: Машиностроение, 1966.
4. Гиршович Т. А. Турбулентные струи в поперечном потоке. М.: Машиностроение, 1993.
5. Никулин М. В. Теплообмен струи воздушной завесы // Гидромеханика отопительно-вентиляционных устройств. Казань, 1989.
6. Стронгин А. С., Никулин М. В. Новый подход к расчету воздушно-тепловых завес // Строительство и архитектура. Изв. ВУЗов. 1991. № 1.
7. Справочник проектировщика: Внутренние санитарно-технические устройства. Ч. 3. Вентиляция и кондиционирование воздуха. Кн. 1 / В. Н. Богословский, А. И. Пирумов, В. Н. Посохин и др.; Под ред. Н. Н. Павлова и Ю. И. Шиллера. 4-е изд., перераб. и доп. М.: Стройиздат, 1992.
8. Титов В. П. Особенности струй воздушных завес // Тепловой режим систем отопления, вентиляции, кондиционирования и теплогазоснабжения: Сб. трудов. М.: МИСИ, 1980. № 177.
9. Татарчук Г. Т. Уточнение метода расчета воздушных завес // Отопление и вентиляция промышленных и сельскохозяйственных зданий: Сб. трудов. М.: НИИСТ, Стройиздат, 1966. № 16.
Тел. (095) 504-25-40

Статья опубликована в журнале “АВОК” за №3'2004
Статьи по теме
- К вопросу о расчете воздушных завес
АВОК №7'2003 - Вентиляция и курение. Контроль за качеством воздуха
АВОК №4'2006 - Расчет системы естественной вентиляции
АВОК №6'2013 - Акты, регулирующие пожаровзрывобезопасность помещений и зданий для размещения технологических устройств сетей газораспределения и газопотребления
АВОК №7'2015 - Особенности систем отопления и вентиляции православных храмов
АВОК №2'2017 - Сикстинская капелла. Модернизация системы ОВК для сохранения объекта культурного наследия
АВОК №1'2018 - Системы вытяжной вентиляции в горячем цехе: жировые фильтры
АВОК №6'2019 - Мнение специалиста и ученого: требуются новые критерии проектирования вентиляции
АВОК №2'2021 - Методология коррекции существующих графиков регулирования отпуска тепловой энергии
АВОК №3'2024 - Качество воздуха в жилых зданиях
АВОК №5'1999

















